Розмір і розмірність

1. Чим відрізняються один від одного довжина, площа та об'єм? [ правити ]
2. Уже не довжина, але ще не площа [ правити ]

Початковий варіант статті (М. Г. Іванов, «Розмір і розмірність») опублікований в серпневому номері 2006 року журналу «Потенціал» .

Під мікроскопом він відкрив, що на бліх
Живе, блоху кусає блішки;
На блішки тій блошінка-крихта,
У блошінку же встромляє зуб сердито
Блошіночка, і так ad infinitum.

Джонатан Свіфт

Чим відрізняються один від одного довжина, площа та об'єм? [ правити ]

Всі ми знаємо, що складати між собою величини, виміряні в різних одиницях не можна. Не всі, втім, розуміють чому. Начебто і довжина, і площа, і обсяг вимірюються в метрах, ось тільки в одному випадку метр лінійний, в іншому квадратний, а в третьому кубічний. А яка нам власне різниця?

Різниця проявляється, якщо ми захочемо перейти від метрів до сантиметрам.

1 м = 100 см = 1001 см1,

1 кв. м. = 1 м2 = 1 м × 1 м = 100 см × 100 см = 10 000 см × см = 1002 см2,

1 куб. м. = 1 м3 = 1 м × 1 м × 1 м = 100 см × 100 см × 100 см = 1 000 000 см × см × см = 1003 см3.

Якщо ми складемо квадратні метри з лінійними, то буде не ясно, в чому буде вимірюватися результат, а значить, буде не ясно на яке число множити відповідь при переході від метрів до сантиметрам. Значить, складати довжину і площу не можна.

Не обов'язково змінювати одиницю довжини саме в сто раз.

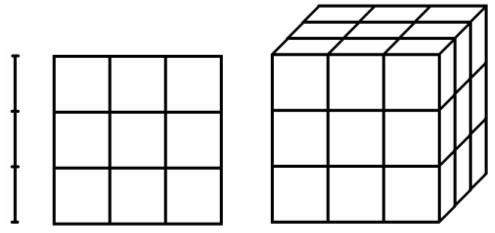
При зміні одиниці довжини в 3 рази одиниця площі зміниться в 3 2 = 3 ⋅ 3 = 9 {\ displaystyle 3 ^ {2} = 3 \ cdot 3 = 9} раз, а одиниця обсягу в 3 3 = 3 ⋅ 3 ⋅ 3 = 27 {\ displaystyle 3 ^ {3} = 3 \ cdot 3 \ cdot 3 = 27} раз. Таким чином, ми можемо «розібрати» великий відрізок на 3 1 {\ displaystyle 3 ^ {1}} відрізків в 3 рази меншою довжини, великий квадрат на 3 2 {\ displaystyle 3 ^ {2}} квадратів в 3 рази менших за лінійними розмірами, великий куб на 3 3 {\ displaystyle 3 ^ {3}} кубиків в 3 рази менших за лінійними розмірами. У всіх перерахованих випадках ми «розбираємо» фігуру на набір рівних між собою за розміром менших фігурок, подібних великий фігурі. Ступінь, до якої зводиться зміна лінійного масштабу, називається розмірністю. Таким чином, відрізок - одномірний, квадрат - двумерен, куб - трёхмерен.

Уже не довжина, але ще не площа [ правити ]

Чи існують фігури, розмірність яких не є цілою, тобто чи може виявитися, що велика фігура розбирається на n {\ displaystyle n} однакових фігурок поменше, кожна з яких подібна до вихідної і відрізняється від неї за лінійними розмірами в k {\ displaystyle k} раз, причому n = k d {\ displaystyle n = k ^ {d}} , Де число d {\ displaystyle d} не є цілим? Виявляється, що такі фігури існують і називаються самоподібними фракталами.

Наприклад, таку фігуру ми можемо «розібрати» на 8 подібних, кожна з яких менше за лінійними розмірами в 3 рази. Ця фігура називається «серветка Серпінського».

Таким чином, 8 = 3 d {\ displaystyle 8 = 3 ^ {d}} , Або (згадавши визначення логарифма) d = log 3 ⁡ 8 = ln ⁡ 8 ln ⁡ 3 ≈ 1, 89 ... {\ displaystyle d = \ log _ {3} 8 = {\ frac {\ ln 8} {\ ln 3 }} \ approx 1 {,} 89 \ dots}

Як будується така серветка Серпінського? Квадрат розбивається на 9 маленьких квадратиків, після чого викидається середній квадратик, потім аналогічна процедура проробляється для кожного з 8 залишилися квадратиків (в 3 рази менших розмірів), потім для кожного з 64 квадратиків (в 9 разів менших розмірів) і так далі (нескінченне число раз).

На кожному кроці площа фігури зменшується на 1 9 {\ displaystyle {\ frac {1} {9}}} , Тобто, якщо ми почали з одиничного квадрата, площа фігури на кроці номер N {\ displaystyle N} дорівнює S = (8 9) N {\ displaystyle S = \ left ({\ frac {8} {9}} \ right) ^ {N}} . А площа виходить в результаті фрактала дорівнює S = 8 9 ⋅ 8 9 ⋯ 8 9 ⋯ = 0 {\ displaystyle S = {\ frac {8} {9}} \ cdot {\ frac {8} {9}} \ cdots { \ frac {8} {9}} \ cdots = 0} . Може бути, там зовсім немає ніякої фігури, раз площа виявилася нульовою? Ні, ми можемо довести, що викинуті виявилися не всі точки квадрата (доведіть це, як вправу, при цьому зручно використовувати трійкову систему числення, для запису координат точок квадрата). Для такої фігури нетривіальне (кінцеве) значення матиме не довжина периметра (нескінченна), і не площа (нульова), а якась міра ( «міра Маньківського»), що вимірюється в одиницях 1 смd Якщо прийняти, що міра Маньківського для квадрата a ⋅ a {\ displaystyle a \ cdot a} дорівнює a d {\ displaystyle a ^ {d}} , То міра серветки Серпінського виявляється дорівнює 1 (на кроці номер N {\ displaystyle N} ми маємо 8 N {\ displaystyle 8 ^ {N}} квадратиків зі стороною (1 3) N {\ displaystyle \ left ({\ frac {1} {3}} \ right) ^ {N}} і міра S M i n k. N = 8 N ((1 3) N) d = 1 {\ displaystyle S _ {\ mathrm {Mink.} \ N} = 8 ^ {N} \ left (\ left ({\ frac {1} {3}} \ right) ^ {N} \ right) ^ {d} = 1} ).

По деякому роздумів корисно узагальнити наведене вище визначення самоподібного фрактала і дозволити йому мати цілі розмірності, наприклад процедура, зображена на наступній серії малюнків, призводить до побудови фігури з розмірністю 1 (Чому?), Але природно вважати цю фігуру фракталом (даний приклад належить Магді Мохамеду ). (Принагідно під фрактали потрапляють і звичайні відрізки, квадрати, трикутники.)

На закінчення наведемо (в якості ілюстрації та вправи по обчисленню розмірності самоподібних фракталів) ще три фігури.

трикутник Серпінського .

Ще один варіант серветки Серпінського .

крива Коха .

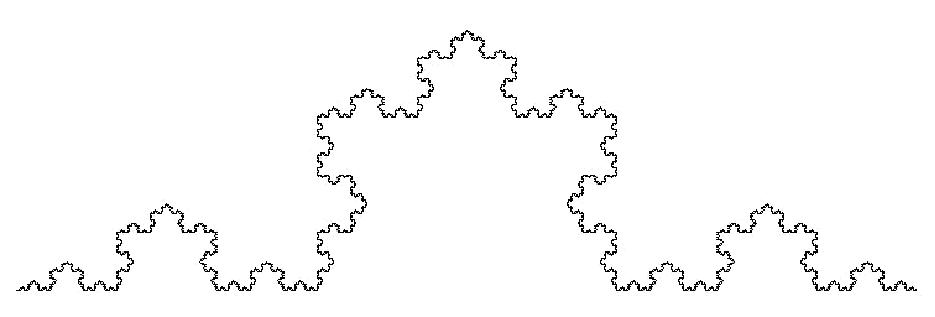
Будується крива Коха так: