Дін а міка маш і н і механ і змов, розділ теорії машин і механізмів, в якому вивчається рух механізмів і машин з урахуванням діючих на них сил. Д. м. І м. Вирішує такі основні завдання: встановлення законів руху ланок механізмів, регулювання руху ланок, знаходження втрат на тертя, визначення реакцій в кінематичних парах, урівноваження машин і механізмів.
Визначення законів руху ланок механізму за заданими характеристиками зовнішніх сил вирішують за допомогою диференціальних рівнянь руху механічної системи або машинного агрегату, що складається зазвичай з двигуна, передавального механізму, робочої машини і іноді керуючого пристрою. Число рівнянь дорівнює числу ступенів свободи цієї механічної системи. У плоских механізмах з одним ступенем свободи для зручності виконання завдання всі сили і маси призводять до одного ланці або точці механізму, які називаються ланкою приведення або точкою приведення. Умовний момент, прикладений до ланки приведення, називається моментом приведення. Момент приведення дорівнює сукупності всіх моментів і сил, прикладених до ланок механізму. Умовний момент інерції ланки приведення називається приведеним моментом інерції. Кінетична енергія ланки приведення дорівнює сумі кінетичних енергій всіх ланок механізму. Аналогічно визначають наведені силу і масу в точці приведення (рис., А):
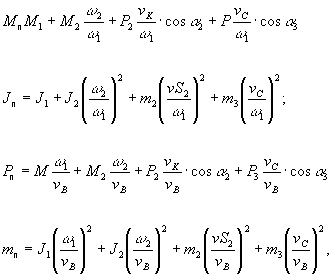
де М п - приведений момент; J п - приведений момент інерції; Р п - приведена сила; m п - зведена маса; M 1, M 2, P 2, P 3 - моменти і сили, прикладені до ланок механізму; w 1, w 2 - кутові швидкості ланок; uB, u C - швидкості точок В і С механізму; uS 2 - швидкість центра ваги ланки 2; uK - швидкість точки До додатки сили P2; a 2 - кут між векторами P 2 і uK; a 3 - кут між векторами P3 і uC. Рівняння руху для даного випадку:
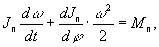
т. е, М п в загальному випадку залежить від часу, положення, швидкості.
Рівняння руху зазвичай є нелінійними. Методів точного рішення їх не існує, тому користуються наближеними графічними, графо-аналітичними і чисельними методами інтегрування. Встановити закон руху механічної системи складніше, якщо враховувати тертя і зазори в кінематичних парах, пружність і змінність мас ланок. Іноді, наприклад при вивченні швидкоплинних процесів в машинах, деякі зовнішні сили не можна вважати заданими, тому що рух механізму може надати зворотний вплив на характеристику цих сил. Наприклад, в деяких режимах з великими прискореннями можна приймати механічну характеристику електродвигуна як задану залежність моменту на валу двигуна від кутової швидкості, тому що на цей момент істотний вплив можуть надати електромагнітні процеси в електродвигуні. В цьому випадку до диференціальних рівнянь руху механічної системи додають диференціальне рівняння електромагнітних процесів в електродвигуні і вирішують їх спільно.
Питання регулювання руху машинного агрегату і управління ним розглядаються в теорії регулювання. Розрізняють несталий, перехідний і сталий режими руху. При сталому режимі швидкості точок механізму є періодичними функціями часу або положення або залишаються постійними. Регулювання усталеного руху зводиться до забезпечення кутової швидкості ланки приведення, що не перевищує допустимого відхилення від її значення. Для цього розраховують і встановлюють на машину спеціальну масу - маховик . Необхідність регулювання несталого руху виникає в тому випадку, коли, незважаючи на неперіодичне зміна зовнішніх сил або мас, в механізмі потрібно підтримувати середню швидкість ланки приведення постійною. Для цього на машину встановлюють спеціальні автоматичні регулятори. Основним завданням при цьому є визначення стійкості руху системи машина - регулятор. Якщо ж швидкість будь-якої ланки (або ін. Параметра) потрібно змінювати по заданому закону (програмі), то в машину вбудовують програмний пристрій. Прикладом може служити програмне керування металорізальними верстатами. Конкретне завдання, що розглядається теорією регулювання, - відшукання оптимальних режимів руху машин (оптимальне управління). Наприклад, визначення руху з найшвидше перехідним режимом при обмеженому прискоренні, т. Е. Оптимального за швидкодією, або руху з мінімумом витрачається в перехідному режимі енергії, т. Е. Оптимального по втратах.
Знаходження непродуктивних втрат в машинах зводиться до визначення втрат на тертя, які є основними і впливають на ефективність роботи машин і механізмів. Ступінь використання енергії в машині оцінюється механічним ККД.
Кінетостатіческій розрахунок механізмів, що виконується при відомому законі руху механізму, проводиться визначенням реакцій в кінематичних парах від всіх заданих зовнішніх сил, а також сил інерції ланок і сил тертя в кінематичних парах. Значення цих реакцій входять в розрахунки ланок на міцність і необхідні для підбору підшипників і розрахунку їх мастила.
Урівноваження машин і механізмів здійснюється раціональним підбором і розміщенням противаг , Що знижують динамічні тиску в кінематичних парах механізмів. На практиці здійснюють уравновешиванием машини на фундаменті (запобігання вібрацій ) Або уравновешиванием обертових мас - балансуванням . Інерційні сили в сучасних швидкохідних машинах досягають великих значень. Змінні по величині і напрямку сили інерції порушують нормальну роботу вузлів машини, є джерелом вібрацій і шуму, які шкідливо впливають на обслуговуючий персонал і порушують нормальну роботу ін. Механізмів і приладів. В вібраційних машинах розраховують умови створення інтенсивних коливань їх виконавчих органів. Динамічні дослідження в машинах безпосередньо пов'язані з розрахунками на міцність і жорсткість елементів машин, які проводяться з метою вибору розмірів і конструктивних форм деталей. Методи таких розрахунків зазвичай викладаються в навчальних дисциплінах: опір матеріалів, динаміка споруд, деталі машин.
Динамічні дослідження проводять також для просторових механізмів з багатьма ступенями свободи. Системи подібного типу мають велику універсальністю виконуваних операцій.
Див. також Машин і механізмів теорія , динаміка споруд , кінетостатікі механізмів , Опір матеріалів , просторовий механізм .
Літ .: Кожешнік Я., Динаміка машин, пров. з чеськ., М., 1961; Зінов'єв В. А., Бессонов А. П., Основи динаміки машинних агрегатів, М., 1964; Артоболевский І. І., Теорія механізмів, 2 вид., М., 1967; Кожевников С. Н., Теорія механізмів і машин, 3 вид., М., 1969.
І. І. Артоболевский, А. П. Бессонов.
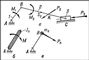
Дія сил і моментів кривошипно-ползунного механізму (а) в ланці приведення (б) і в точці приведення (в): 1 - кривошип; 2 - шатун: 3 - повзун; М - приведений момент МП; А - нерухома опора.




