Гідростатичний тиск. Як відомо, в яка покоїться рідини можливий лише один вид напруг - напруження стиску, т. Е. Гідростатичний тиск. Гідростатичний тиск в рідині має наступні дві властивості:
- На зовнішній поверхні гідростатичний тиск завжди направлено по нормалі, всередину розглянутого об'єму рідини.
Це властивість безпосередньо випливає з визначення тиску як напруги від нормальної стискає сили. Під зовнішньою поверхнею рідини розуміють не тільки поверхні розділу рідини з газоподібної середовищем або твердими стінками, але і поверхні елементарних обсягів, подумки виділяються із загального обсягу рідини.
- У будь-якій точці всередині рідини гідростатичний тиск в усіх напрямках однаково, т. Е. Тиск не залежить від кута нахилу майданчика, на яку воно діє в даній точці. Для доказу цього властивості виділимо в нерухомій рідини елементарний об'єм у формі прямокутного тетраедра з ребрами, паралельними координатним осях і відповідно рівними dx, dy і dz (рис. 2.1).
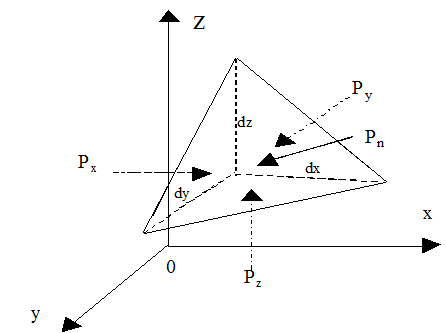
Мал. 2.1
Нехай на виділений об'єм рідини діє одинична масова сила, складові якої рівні X, Y і Z. Позначимо через px гідростатичний тиск, що діє на грань, нормальну до осі 0x, через py тиск, що діє на грань, нормальну до осі 0y, і т. д.
Гідростатичний тиск, що діє на похилу грань, позначимо через pn, а площа цієї грані - через dS. Всі ці тиску спрямовані по нормалям до відповідних майданчиків.
Складемо рівняння рівноваги виділеного об'єму рідини спочатку в напрямку осі 0x.
Проекція сил тиску на вісь 0x дорівнює:
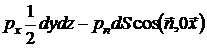
Маса тетраедра дорівнює добутку його обсягу на щільність, т. Е.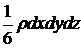 
, Отже, масова сила, що діє на тетраедр уздовж осі 0x, дорівнює:
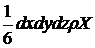
Рівняння рівноваги тетраедра запишемо в наступному вигляді:
Розділимо це рівняння почленно на площу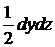 
, Яка дорівнює площі проекції похилій грані dS на площину y0z, і, отже:
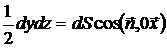
Будемо мати:
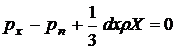
При прагненні розмірів тетраедра до нуля останній член рівняння, що містить множник dx, буде також прагнути до нуля, а тиску px і pn залишатимуться кінцевими величинами. Отже, в межі отримаємо, що px - pn = 0 або px = pn. Аналогічно складаючи рівняння рівноваги уздовж осей 0y і 0z, після таких же міркувань отримаємо, що py = pn, pz = pn, т. Е.
px = py = pz = pn (2.1)
Так як розміри тетраедра dx, dy і dz були взяті довільно, то і нахил площадки dS довільний, і, отже, в межі при стягуванні тетраедра в точку тиск в цій точці в усіх напрямках буде однаково. Розглянуте властивість тиску в нерухомій рідини має місце також при русі ідеальної рідини. При русі ж реальної рідини виникають дотичні напруження, внаслідок чого тиск у реальної рідини зазначеним властивістю, строго кажучи, не володіє.
