Щоб не загубилася нитка обговорень, ось знайдена в процесі тестування R помилка розрахунку квантилів нецентрального t-розподілу.
наприклад:
> N <- 10> k <- seq (0,1, by = 1 / n)> nt_pdf <-dt (k, 10,8, log = FALSE)> nt_cdf <-pt (k, 10,8, log = FALSE)> nt_quantile <-qt (nt_cdf, 10,8, log = FALSE)> nt_pdf [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e -13 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11> nt_cdf [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12> k [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0> nt_quantile [1] -Inf -1.340781e + 154 -1.340781e + 154 -1.340781e + 154 -1.340781e + 154 -1.340781e + 154 [7] -1.340781e + 154 7.000000e-01 8.000000e-01 9.000000e-01 1.000000e +00
Для розрахунку ймовірності нецентрального T-розподілу Стьюдента в мові R використовується алгоритм AS 243, запропонований Lenth [6]. Перевагою цього методу є швидкий рекурентний розрахунок членів нескінченної низки з неповною бета-функцій. Але в статті [7] було показано, що через помилки оцінки точності при підсумовуванні членів ряду даний алгоритм призводить до помилок (таблиця 2 в статті [7]), особливо для великих значень параметра нецентральних delta. Автори статті [7] запропонували скоригований алгоритм рекурентного розрахунку ймовірності нецентрального T-розподілу.
У нас в статистичної бібліотеці MQL5 використовується правильний алгоритм для розрахунку ймовірностей зі статті [7], що дає точні результати.
Крім того, в мові R спосіб визначення щільності для розподілів Gamma, ChiSquare і Noncentral ChiSquare в точці x = 0 призводить до нескінченних виразами:
> Dgamma (0,0.5,1) [1] Inf> dchisq (0, df = 0.5, ncp = 1) [1] Inf> dchisq (0, df = 0.5, ncp = 0) [1] Inf
Таким чином, виходить, точка x = 0 в R включена в область визначення виразу для густини і рішенням є граничні значення.
В даному випадку граничним значенням в точці x = 0 є нескінченність. При такому підході в результаті інтегрування від 0 до x> 0 через розбіжність в точці x = 0 ймовірності повинні бути нескінченними.
Однак результатом розрахунку ймовірностей (наприклад, для x = 0.1) є кінцеві вирази:
> Pgamma (0.1,0.5,1) [1] 0.3452792> pchisq (0.1, df = 0.5, ncp = 0) [1] 0.5165553> pchisq (0.1, df = 0.5, ncp = 1) [1] 0.3194965
Незважаючи на те, що в точці x = 0 щільність вважається нескінченною, результати розрахунку ймовірностей в R не є нескінченними, вони збігаються зі значеннями Wolfram Alpha ( Gamma , ChiSquare , NoncentralChiSquare ).
Для уникнення проблем з інтеграцією функцій, що звертаються в нескінченність в при x = 0, в Wolfram Alpha (Mathematica) і Matlab щільність в точці x = 0 дорівнює 0 за визначенням:
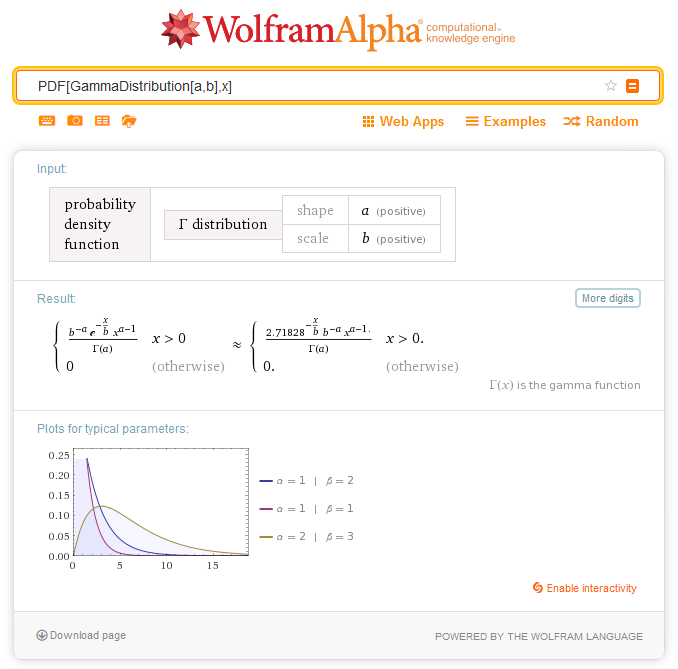
Мал. 3. Визначення щільності ймовірності розподілу Gamma в Wolfram Alpha
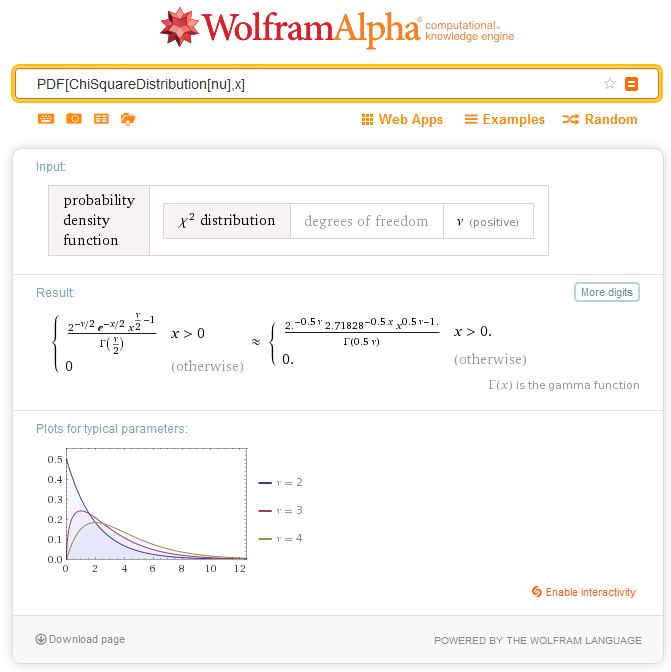
Мал. 4. Визначення щільності ймовірності розподілу ChiSquare в Wolfram Alpha
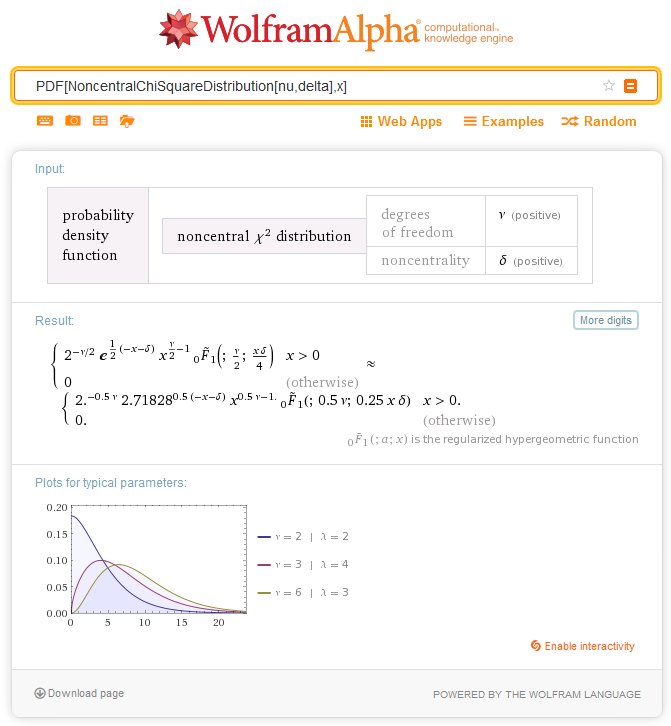
Мал. 5. Визначення щільності ймовірності розподілу Noncentral ChiSquare в Wolfram Alpha
Ми вважаємо такий похід правильним. Він дозволяє уникнути невизначеностей у визначенні щільності ймовірності і вирішити проблему з нескінченними значеннями, які можуть виникнути при інтегруванні щільності ймовірності.
З цієї причини в точці x = 0 щільності даних розподілів вважаються рівними нулю за визначенням, а не нескінченності, як в R.
Щоб бути впевненими в точності розрахунків і дати можливість стороннім розробникам перевірити якість бібліотеки, ми включили кілька unit test скриптів в поставку.
література
- The R Project for Statistical Computing .
- Балакрішнан Н., Джонсон Н.Л., Коц С. "Одномірні безперервні розподілу: частина 1." М .: БИНОМ. Лабораторія знань, 2014.
- Балакрішнан Н., Джонсон Н.Л., Коц С. "Одномірні безперервні розподілу: частина 2." М .: БИНОМ. Лабораторія знань, 2014.
- Джонсон Н.Л., Коц С., Кемп А. "Одномірні дискретні розподілу" , М .: БИНОМ. Лабораторія знань, 2014.
- Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions" , 4th Edition, John Wiley and Sons, 2011 року.
- Lenth, RV, "Cumulative distribution function of the noncentral t distribution" , Appled Statistics, vol. 38 (1989), 185-189.
- D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient" , Computational Statistics & Data Analysis, 43, (2003), 249-267




