Г л а в а 12
У. Д. Хейз
У гіперзвукової аеродинаміки широко використовується формула
відома як формула тиску Ньютона. Тут C p - коефіцієнт тиску;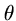 
- місцевий кут нахилу контуру тіла по відношенню до напрямку невозмущенного потоку. Ця формула названа ім'ям Ісаака Ньютона, який відкрив її на основі дедуктивних міркувань (див. Його «Математичні початки натуральної філософії» [ 1 ]).
Найбільш доступним першоджерелом праць Ньютона є англійський переклад Кеджорі-Мотта третього видання «Почав» [ 1 ]. Тут ми коротко відзначимо основні положення відповідних пропозицій з II книги «Начал».
а) Пропозиція 23. Постулюється корпускулярна модель газу, який підкоряється закону Бойля і в якому пружність обумовлюється силами відштовхування між частинками. Це основна модель для подальшого дослідження газів.
б) Пропозиції 32 і 33. Встановлюється подоба систем для зазначеної вище моделі газу, еквівалентне нашому звичайному подобою по числу Маха; при цьому тиск вважається пропорційним щільності і квадрату швидкості.
в) Пропозиція 33. Наслідки II і III. Ньютон робить висновок, що при дуже великих швидкостях можна знехтувати пружністю газу. Це еквівалентно закону незалежності течії від числа Маха або законом подібності Осватіча для моделі Ньютона.
г) Пропозиція 35. Без урахування пружності газу Ньютон досліджував його взаємодія зі стінкою в разі дзеркального відображення частинок (випадок 1) і в разі непружного нормального зіткнення зі збереженням тангенціального кількості руху (випадок 2). Отримані результати в останньому випадку еквівалентні рівняння ( 1 ), А в першому - рівняння ( 1 ) З коефіцієнтом 4 замість 2.
д) Пропозиція 34. Оскільки тиск пропорційно квадрату синуса, то опір сфери вдвічі менше опору кругового циліндра того ж діаметру, вісь якого направлена по потоку.
е) Повчання до пропозиції 34. З трьох представлених тут результатів найбільш цікавий останній. Тут Ньютон вказує форму тіла обертання мінімального опору з заданими діаметром підстави і довжиною. Перший же результат, що визначає форму усіченого конуса мінімального опору з заданими основою і висотою, важливий для нас в тому сенсі, що він визначає граничний випадок для тел оптимальної форми. Коли відношення висоти конуса до площі його лобового підстави прагне до нуля, оптимальний кут нахилу його утворює прагне до 45 °.
Більш детально ці теореми Ньютона розглянуті в роботі [ 2 , Гл. III].
Тут ми зупинимося на результатах, викладених в повчанні до пропозиції 34, де описана форма тіла обертання мінімального опору, отримана за формулою тиску Ньютона. Введемо звичайні позначення: x - координата в напрямку невозмущенного потоку; y - радіальна координата; y (x) - меридіональний контур тіла;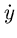 
- похідна dy / dx; індекси i, f - початкова і кінцева точки контуру. Нехай тіло має плоску носову частину. Помічаючи, що кут нахилу контуру тіла задовольняє співвідношенню sin2 = 
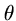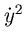/ (1 + 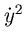) І диференціал площі в поперечній площині дорівнює 2 
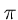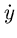y dx, ми будемо мінімізувати функціонал
що являє собою суму інтеграла і функції, що залежить від координати початкової точки контуру. Цей функціонал розглядається при наступних граничних умовах: x i = 0, x f = l, y f = t / 2, (3) де l - довжина тіла; t - діаметр основи (міделю); радіус носика тіла y i, знаходиться з рішення варіаційної задачі. Видно, що при використанні звичайних методів варіаційного обчислення рівняння Ейлера допускає наступний перший інтеграл: Константа в цьому виразі обчислена з умови трансверсальності, з якого також випливає, що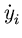 
= 1. Більш докладно це рішення і другий інтеграл, що залежить від параметра, розглянуті в гл. 16 і в роботі [ 3 ]. Перший інтеграл ( 4 ) Отримано Ньютоном в його повчанні до пропозиції 34.
У самих «Засадах» можна знайти навіть натяку на те, як Ньютон отримав свій результат. Рішення було знайдено в його листуванні; воно обговорюється Кеджорі в додатку до роботи [ 1 ] (Примітка 35). Використаний їм метод можна застосувати до будь-якого завдання, в якій основна функція F (x, y, 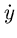) Не залежить від x або від y.
Для пояснення методу Ньютона скористаємося рис. 1, де відрізок BC зображує вісь x між початковою і кінцевою точками, BG одно y i, CD одно y f, а контур GgNnD - шукана екстремали. Позначимо через m довільну точку на осі x і приймемо відрізок on = hg як диференціала відстані, тоді Gg і Nn можна буде наближено розглядати як прямолінійні відрізки. Ньютон при варіюванні вважав, що bM і Bb + Mm фіксовані, а величина z = (Mm - Bb) / 2 розглядалася як незалежна змінна. При варіюванні z відрізок кривої між точками g і N просто зміщується в поперечному напрямку. Інтеграл, який можна мінімізувати, виражається через z, а його екстремум по z знаходиться шляхом прирівнювання нулю похідною по z. Ця процедура можлива внаслідок того, що частка, яку вносить відрізком gN, не залежить від z. Результатом є перший інтеграл ( 4 ) З довільної сталої.
Частина тіла, позначена через BGgb, є усіченим конусом. До нього можна застосувати перший результат повчання, що полягає в тому, що кут gGh має дорівнювати 45╟. Цей результат дає можливість визначити постійну в першому інтегралі і отримати рівняння ( 4 ).
Ясно, що результат Ньютона, опублікований в 1687 р, є основою загального методу варіаційного обчислення для вирішення нетривіальних завдань. Класичну задачу про Брахістохрона І. Бернуллі вирішив в 1697 р і запропонував її Ньютону в листі [ 4 ]. Ньютон вирішив задачу за 12 годин. Швидкість, з якою він міг вирішити цю задачу, на перший погляд здається дивною. Однак метод, розроблений Ньютоном раніше, можна було безпосередньо застосувати до цієї нової задачі, і тому така швидкість рішення здається цілком природною. Завдання про Брахістохрона подібна завданню Ньютона про тіло мінімального опору, за винятком того, що другий інтеграл в ній зводиться до квадратури, що дозволяє представити рішення в явному вигляді 1) .
Спосіб варіювання, використаний Ньютоном, можна інтерпретувати як варіювання величини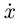 
(Y) в інтеграл
де 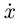- похідна dx / dy. У цьому виразі, яке еквівалентно функціоналу ( 2 ), Ролі залежною і незалежною змінних помінялися місцями. Хоча Ньютон досліджував тільки слабкі варіації, ясно, що його метод також застосуємо і для сильних варіацій. Цей метод можна використовувати для підтвердження результату Лежандра про те, що екстремали ( 4 ) НЕ мінімізує інтеграл ( 5 ), Якщо x може приймати як позитивні, так і негативні значення.
Тепер повернемося до питання про можливість застосування формули тиску Ньютона до реальних течій газу [ 2 ], [ 5 ]. Ньютоновская модель газу по суті являє собою модель розрідженого газу, тоді як дійсний механізм взаємодії молекул газу з твердими границями в принципі відрізняється від неї. Формула тиску Ньютона наближено справедлива для холодних тіл при дуже великих швидкостях, але несправедлива для нагрітих тел. Однак має велике значення те, що в розрідженому потоці на тіло діють великі дотичні напруження, які не враховуються формулою тиску Ньютона. Для газів з великою щільністю ця формула тиску багато років тому розглядалася балістики як емпірична формула з невідомої константою. У 1930 р було визнано, що рівняння ( 1 ) Може бути придатним для течій газу з великою швидкістю. Як показав Буземан [ 6 ], Необхідні умови для цього полягають у тому, щоб а) відношення щільності невозмущенного потоку до щільності за передній ударною хвилею було дуже мало і б) кривизна контуру тіла в напрямку невозмущенного потоку була мала.
В даний час формула тиску Ньютона ( 1 ) Зазвичай застосовується для визначення тиску на тілах різної форми при обтіканні їх потоком газу з великою швидкістю. Застосування цієї формули носить чисто емпіричний характер, так як одночасно обидва умови а) і б) рідко задовольняються навіть наближено. Помилки, зумовлені порушенням умов а) і б) для опуклих тіл, мають тенденцію до взаємного знищення. Саме цим можна пояснити експериментальне підтвердження формули тиску Ньютона.
Для будь-яких додатків важливо мати на увазі емпіричний характер формули ( 1 ). Вона не може бути повністю застосовна для тіл довільної форми, а також для розрахунку змін тиску на тілі, викликаних як завгодно малими змінами його форми. Таким чином, застосування формули ( 1 ) Для вирішення задачі про тілах оптимальної форми залишає деякі сумніви.
Яких результатів в такому випадку ми можемо очікувати від рішень варіаційних задач із застосуванням формули тиску Ньютона? Ми можемо очікувати, що виходять в результаті рішення варіаційних задач тіла випуклої форми повинні бути цілком подібні тіл істинно оптимальної форми. Крім того, вплив різних умов на розраховану форму тіла має бути принаймні якісно вірно. Таким чином, якісні оцінки можна отримати без сумніву.
ЛІТЕРАТУРА
- N e w t o n I., Mathematical principles of natural philosophy, A. Motte's translation revised by F. Cajori, University of California Press, Berkeley, California, 1934. Є російський переклад: Н ь ю т о н І., Математичні початки натуральної філософії , Переклад з лат. з передмовою і доповненням акад. А. Н. Крилова, СПБ, 1915-1916; см. також К р и л о в А. Н., Собрание трудов, т. 7, вид. АН СРСР, М.-Л., 1936.
- X е й з У. Д., П р о б с т і н Р. Ф., Теорія гіперзвукових течій ІЛ, М., 1962.
- Е g g e r s AJ, Jr., R e s n i k o f f MM , D e n n i s D. Н., Bodies of revolution having minimum drag at high supersonic airspeeds , NACA, Report 1306, 1957.
- A n t h o n y HD, Sir Isaac Newton, Collier Books, Riverside, New Jersey, 1961.
- Ч е р н и й Г. Г., Течії газу з великою надзвуковою швидкістю , Физматгиз, М., 1959.
- B u s e m a n n A., The motion of liquids and gases (in German), Hand-wörterbuch der Naturwissenschaften, v. 4, Gustav Fischer, Jena, 1933.
Хейз У.Д. Формула тиску Ньютона // Теорія оптимальних аеродинамічних форм: Зб. статей під ред. А.Міеле, пров. з англ. М .: "Світ", 1969, с. 197-202
Стаття в вигляді, підготовленому для друку у вигляді міні-зошити: 
haiz_ps.rar (129 K)
[email protected] 
1)
У задачі Ньютона рішення також можна уявити в явній формі у вигляді зворотної функції. - Прим. ред.
