Моделювання електромагнітного нагрівання підземних кабелів

1. Властивості підземних силових кабелів
2. Моделювання електромагнітних полів в підземному кабелі
3. Аналіз зростання температури в системі за допомогою COMSOL Multiphysics®
4. Використання граничного умови Thin Layer (Тонкий Шар)
5. Моделювання навколишнього простору для термічної завдання
6. До вирішення моделі
7. Заключні зауваження по моделюванню електромагнітного нагрівання підземних кабелів
8. додаткові ресурси

Повітряні силові лінії можна помітити повсюдно, але також існує велика кількість підземних силових кабелів, які ми не бачимо. Перевага останніх - це захист від вітру і снігу, а також менше електромагнітне випромінювання, завдяки екрануванню. Одним з ключових недоліків підземних кабелів є їх істотний перегрів, який призводить до пошкодження ізоляції і, в кінцевому підсумку, виходу з ладу. Давайте подивимося, як змоделювати і дослідити електромагнітний нагрів в програмному забезпеченні COMSOL Multiphysics®.

Властивості підземних силових кабелів

Типовий підземний трифазний електричний кабель складається з пучка трьох провідних жив. Кожна жила складається з безлічі проводів, скручених разом і стислих, тим самим забезпечуючи хороший електричний контакт. Також жила може мати екранування, наприклад з металевої фольги. Полімерний матеріал між житловою і екраном забезпечує електричну ізоляцію. Як електричні ізоляторів використовується пресована папір, рідини і навіть стислі гази. Потім ізольований пучок жив поміщається в ще один діелектрик, потім в металевий кожух і зовнішнє полімерне покриття, яке захищає кабель від навколишнього середовища.

Зліва: Підземний трифазний електричний кабель. Справа: Поперечний перетин трифазного кабелю під землею.

Змінний струм, що проходить через кабель, створює змінне магнітне поле, яке індукує струми в жилах, в металевому кожусі і фользі. Вихрові струми приводять до комбінованого нагріву: джоулева і індукційному . Кабель починає нагріватися, що може привести до його виходу з ладу, тому в наших інтересах побудувати Інтелектуальне розрахункову модель.

Електричний розрахунок кабелю досить простий. Зазвичай ми знаємо всі властивості матеріалу (електропровідність, магнітну і діелектричну проникність) кабелю, а також величину і частоту протікає через нього струму. Однак, ми лише приблизно знаємо електричні властивості навколишнього грунту.

Теплові властивості також невідомі. Вони змінюються залежно від складу грунту і вмісту в ній вологи. Навіть в кабелі, в якому ми знаємо всі властивості матеріалу, можуть бути тонкі шари невідомого матеріалу і невеликі повітряні зазори, які впливають на максимальну температуру.

Давайте дізнаємося, як моделювати такі типи кабелів за допомогою COMSOL Multiphysics.

Моделювання електромагнітних полів в підземному кабелі

Припустимо, що підземні кабелі є досить довгими, а навколишнє середовище щодо однорідна. Ці припущення дозволяють спростити нашу модель. Будемо розглядати поперечний 2D зріз, аналогічний показаному на малюнку вище. Ми знаємо, що трифазний струм в кабелі протікає із заданою частотою. Амплітуда струму також відома.

Будемо розглядати кожну з трьох жив як єдиний домен, вважаючи, що мідні дроти, скручені разом, мають хороший електричний контакт. Таким чином, ми використовуємо три різних вузла Котушка (Coil), як показано на скріншоті нижче. Протікає через жили ток задаємо в наступному вигляді: 1 [kA] * exp (-i * 120 [deg]).

Амплітудне значення струму - 1кА, зрушення фаз - 120 °.

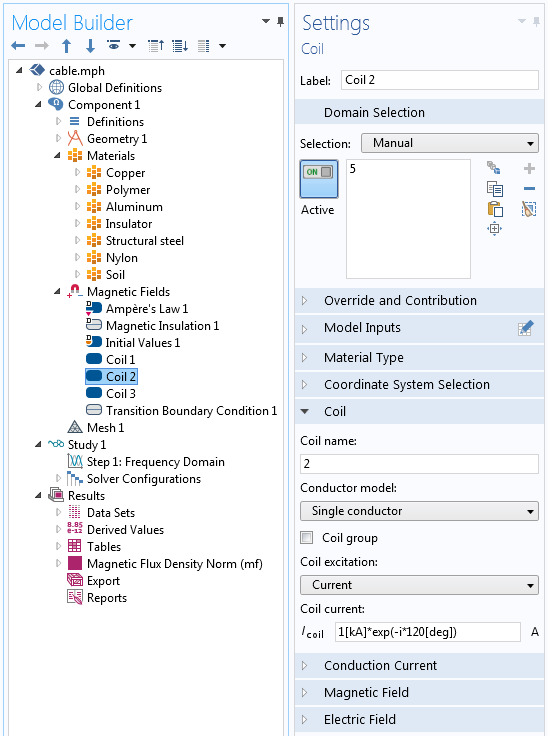
У вузлі Котушка задаємо значення струму, що протікає через жилу. У двох інших жилах протікає такий же струм, але зміщений по фазі на 120 °.

Далі задаємо тонкий шар металевого екранування. Якщо товщина цього шару мала в порівнянні з іншими розмірами, то можна поставити це шар металу за допомогою Перехідної граничної умови (Transition Boundary Condition), як показано нижче. Це гранична умова дозволяє задати товщину шару і його властивості на внутрішньому кордоні моделі. Даний вузол полегшує побудова геометрії, при цьому додатково зникає необхідність в побудові сітки на цій ділянці.

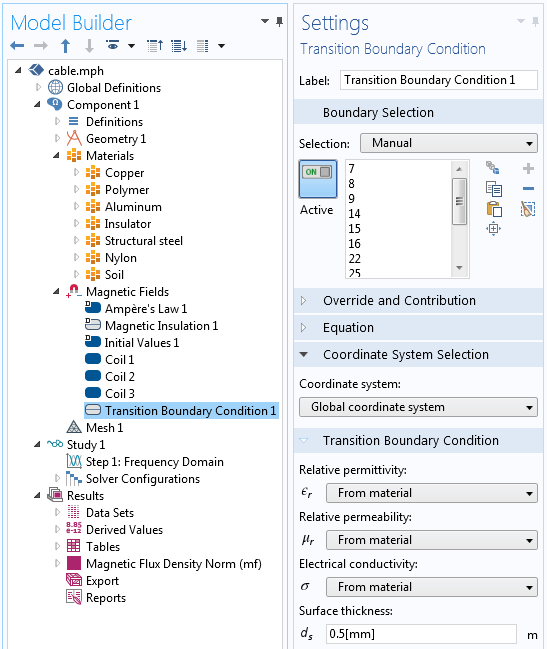
Вузол Перехідний гранична умова (Transition Boundary Condition), в якому задається товщина шару і його властивості.

Магнітні поля можуть поширюватися за межами кабелю. Так як ми хочемо знати, як швидко поля загасають, необхідно також моделювати область грунту навколо кабелю. Про те, як вибрати розмір цієї області ітераційним методом (провівши додаткове дослідження по збіжності), прочитайте в попередній статті блогу на тему вибору граничних умов для моделювання котушок . Результати моделювання зображені на малюнку нижче. Стрілками показано магнітне поле, кольоровим градієнтом - усереднені втрати. Саме ці втрати призводять до підвищення температури.

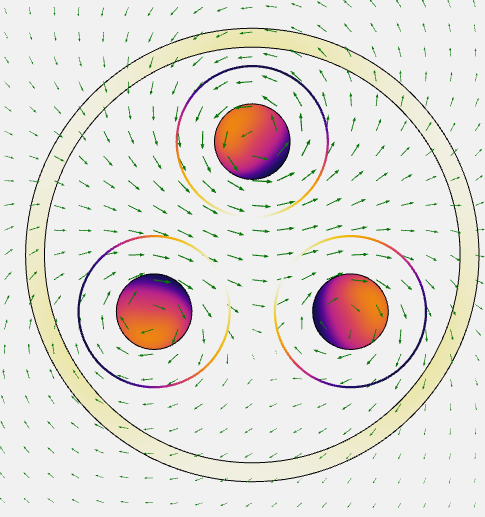
Втрати в жилах і в екранованої оболонці, стрілками показано магнітне поле. Довжина стрілок логарифмически масштабується щодо напруженості магнітного поля.

Аналіз зростання температури в системі за допомогою COMSOL Multiphysics®

Моделювання росту температури здається відносно простим - ми просто додаємо розраховані втрати в теплову модель. Додаємо в модель фізичний інтерфейс Heat Transfer in Solids (Теплопередача в твердих тілах), а також в вузлі Multiphysics (Мультіфізіка) використовуємо встановлені зв'язки, які дозволять нам зв'язати електромагнітну і теплову завдання. Для розрахунку електромагнітної завдання в частотної області можна використовувати дослідження Frequency-Stationary (Комбінований частотно-стаціонарний) або Frequency-Transient (Комбінований частотно-нестаціонарний), при цьому теплова задача буде розрахована в сталому режимі або в тимчасовій області.

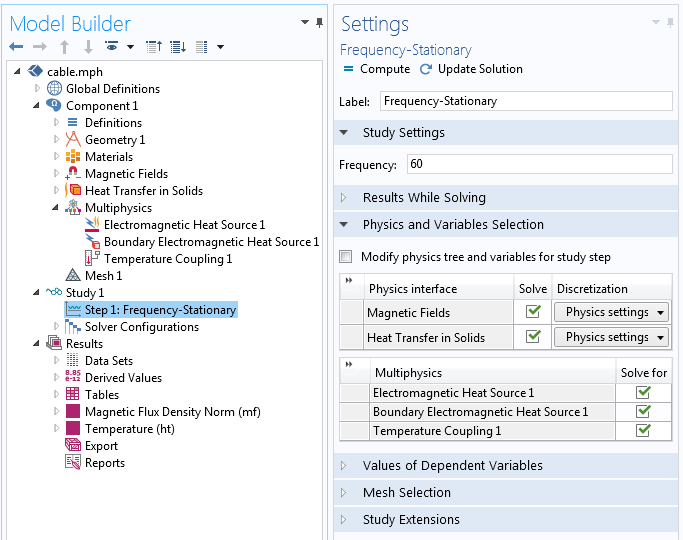
Налаштування Frequency-Stationary решателя і список мультіфізіческіх зв'язок, які потрібні для двосторонньої інтеграції електромагнітного і теплового розрахунків.

Використання граничного умови Thin Layer (Тонкий Шар)

Незважаючи на те, що теплова модель здається простою, є ряд моментів, які необхідно мати на увазі поряд з особливостями програмного забезпечення. Наприклад, в кабелі є кілька тонких шарів різних матеріалів, а саме: екрани кожної жили і полімерне покриття всього кабелю. Для них ми будемо використовувати граничну умову Тонкий шар (Thin Layer). За допомогою цього вузла шар матеріалу можна задати трьома різними наближеннями: Thermally thin approximation (Наближення термічного тонкого шару), Thermally thick approximation (Наближення термічно товстого шару) і General (Загальний випадок), як показано на скріншоті нижче.

Наближення Thermally thin approximation використовується, коли шари матеріалу мають відносно велику теплопровідність в порівнянні з навколишнім середовищем, в той час як наближення Thermally thick approximation краще використовувати для шарів матеріалу з відносно більш низьку теплопровідність. Наближення General використовується для будь-яких проміжних шарів, де є характерні температурні градієнти, як перпендикулярні, так і тангенціальні до шару матеріалу. Ці опції дозволяють задати товщину і властивості шару, а наближення General дозволяє додатково поставити до п'яти різних шарів.

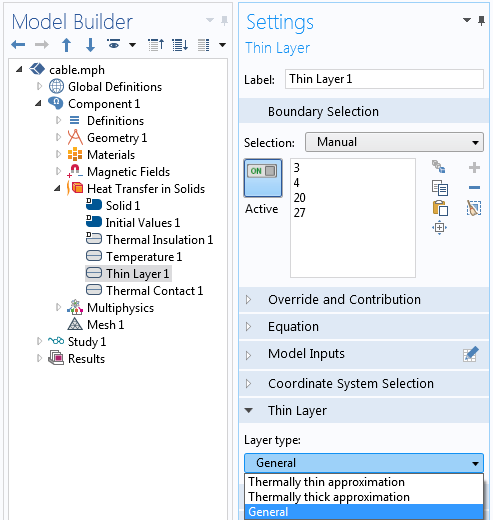
Гранична умова Thin Layer (Тонкий шар).

Гранична умова Thin Layer (Тонкий шар) підходить для чітко визначених шарів матеріалу з відомою товщиною і властивостями. Також необхідно враховувати теплове опір, що виникає при контакті двох матеріалів. Теплопередача при контакті шорсткуватих поверхонь виникає, якщо є:

• Тепловіддача шляхом теплопровідності (кондуктивний теплообмін) при стисненні твердих матеріалів разом
• Тепловіддача шляхом теплопровідності через тонкий шар повітря
• Радіаційний теплообмін між відкритими поверхнями

Ці ефекти можуть бути задані за допомогою вузла Thermal Contact (Термічний контакт), як показано на скріншоті нижче.

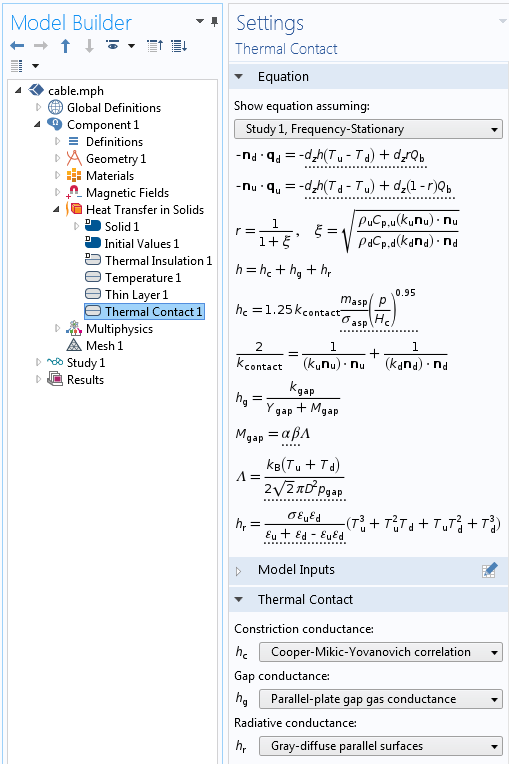
Вузол Thermal Contact (Термічний контакт) і рівняння, які вирішуються при моделюванні.

Контактний тиск сильно впливає на кондуктивний теплообмін між твердими тілами. Його можна знайти, виконавши структурний аналіз, як показано в навчальних моделях:

Моделювання навколишнього простору для термічної завдання

Далі необхідно врахувати температуру навколишнього середовища, яка сильно варіюється, що безпосередньо впливає на температуру кабелю. Теплопровідність навколишнього грунту, бетону і грунту коливається від 0.1 до 5 W / m / K, щільність - від 1000 kg / m3 для м'яких і до 3000 kg / m3 для твердих порід. Їх питома температура також варіюється від ~ 500 до 1500 J / kg / K. Крім того, ці значення постійно змінюються. Наприклад, теплопровідність сухого і вологого піску може на порядок відрізнятися: від ~ 0.2 до 4 W / m / K. Також корисно ввести коефіцієнт теплопровідності , Який визначається як \ alpha = \ frac {k} {\ rho C_p} і варіюється для цих матеріалів приблизно від 10 ^ {- 8} -10 ^ {- 5} m ^ 2 / s.

На додаток до сильних змін термічних властивостей грунту, теплове гранична умова на поверхні також рідко чітко визначено. Присутній як конвективное, так і радіаційне охолодження. Інтенсивність цього охолодження багато в чому залежить від локальних і короткочасних властивостей на поверхні. Наприклад, опале листя або пухкий сніг можуть служити хорошим шаром теплової ізоляції, який складно розрахувати кількісно з будь-якої точністю. На щастя для нас, кабелі зариті досить глибоко, так часто можна знехтувати цими змінами на поверхні. Таким чином, розумно поставити тепловий баланс на поверхні, як комбінацію з трьох граничних умов:

1. Гранична умова Heat Flux (Тепловий Потік), що задає сонячний тепловий потік на основі широти і пори року
2. Ще одне граничне умова Heat Flux (Тепловий Потік), що задає конвективное охолодження до середньої температури навколишнього повітря.
3. Гранична умова Diffuse Surface (розсіюючої Поверхня), що задає радіаційне охолодження до еквівалентної температури неба

Сонячний тепловий потік і температуру навколишнього повітря можна задати приблизно або на основі бази даних метеорологічних станцій ASHRAE (American Society of Heating, Refrigerating, and Air-Conditioning Engineers), як ми описали в одній з минулих статей нашого блогу . Температура неба коливається приблизно від 230 K до 285 K (-45 ° C до 10 ° C) в залежності від хмарності і температури повітря. Коефіцієнт випромінювання з поверхні землі - 0.8-0.95. Також слід враховувати товщину і глибину нашого розрахункового теплового домену.

Нам необхідно моделювати досить велику область грунту, щоб граничні умови не впливали на результати. Для температурних навантажень, які в часі змінюються синусоидально з періодом \ tau, відстань D від кордону, на якій коливання температури зменшується приблизно на 90% щодо коливань на поверхні, задається як: D = \ sqrt {\ frac {\ tau \ alpha} { 2 \ pi}}.

Припустимо, що температурні граничні умови змінюються протягом року синусоидально і значення теплопровідності досить велике. Як показує практика, таку область можна моделювати, як домен, який простягається не менше ніж на вісім метрів нижче поверхні і в три рази перевищує глибину укладання кабелю з кожного боку. Гранична умова типу Теплова ізоляція задається на вертикальних межах, а гранична умова з фіксованою температурою - на нижній межі. Гранична умова Температура використовується для завдання на нижній межі температури, яка дорівнює середньому значенню температурі поверхні протягом всього року. Це добре наближення для великої маси грунту.

Також можна досліджувати більшу область грунту, щоб оцінити, чи дуже змінилися максимальні температури. Звичайно, якщо є особливості в прилеглому ґрунті, наприклад, водогони або фундамент будівель, вони повинні бути враховані в моделі.

До вирішення моделі

Для розрахунку цієї моделі можна скористатися типом дослідження Frequency-Stationary (Комбіноване частотно-стаціонарне) або Frequency-Transient (Комбіноване частотно-нестаціонарне). Обидва дослідження дозволяють проводити рішення системи рівнянь Максвелла в частотної області, а теплової задачі - як стаціонарної або залежної від часу. При стаціонарному вирішенні потрібна деяка обережність в обробці результатів. Стаціонарний аналіз передбачає, що всі теплові перехідні процеси припинилися, що є серйозним припущенням. Такі результати слід інтерпретувати з особливою уважністю. З іншого боку, рішення перехідною завдання дозволить враховувати всі зміни навколишнього середовища і її зовнішній вплив. Результатом такого розрахунку стануть не тільки максимальні температури, але і діапазони часу, протягом яких різні матеріали перебували при різних температурах.

На скріншоті нижче показана настройка моделі і вибіркові результати.

Теплова модель і достовірні результати температури кабелів. Так як магнітні поля швидко згасають, вони розраховуються тільки для невеликої області навколо кабелю.

Заключні зауваження по моделюванню електромагнітного нагрівання підземних кабелів

У цій статті ми продемонстрували функціонал COMSOL® і основні методи, які можна використовувати при моделюванні зростання температури в підземних силових кабелях. При вирішенні таких завдань враховуйте, що з огляду на змінюються параметрів теплової середовища, невідомих властивостей грунту і навіть невеликих повітряних зазорів або зазорів в самому кабелі підсумкове рішення може значно відрізнятися. Звичайно, COMSOL Multiphysics (при наявності розширень AC / DC і Теплопередача) - відмінний інструмент для моделювання таких завдань і обліку всіх змін вхідних даних.

Зацікавлені у використанні COMSOL Multiphysics для моделювання електромагнітного нагрівання?

додаткові ресурси

• Дізнайтеся більше про електромагнітному моделюванні в нашому блозі: