Челябінський державний університет
Інститут радіотехніки й електроніки РАН, 125009 Москва, Росія
Дослідження відбивної здатності різних речовин є актуальним у зв'язку з потребою в відбивають і поглинають електромагнітне випромінювання матеріалах. Ці матеріали широко застосовуються у вимірювальній та контрольної техніці, техніці зв'язку, радіолокації, медицині та інших областях науки і техніки. Зазвичай завдання щодо зменшення КО ЕМВ намагаються вирішити шляхом вирівнювання хвильових опорів всередині і поза середовищем або, зокрема, при падінні хвилі з вакууму, шляхом вирівнювання величин діелектричної та магнітної проникності матеріалу. При цьому потрібно змінювати склад речовини, що є досить складною проблемою. В даний час існують різні підходи до управління КО конструкційним шляхом [ 1 , 2 ]. Однак є й інша, більш проста можливість управління КО ЕСВ - за рахунок зміни динамічної магнітної проникності магнітовпорядкованих речовин і простих змін структури у вигляді різного чергування взаємодіючих магнітних і немагнітних шарів.
У роботах [ 3 , 4 ] При обліку взаємодії трьох підсистем феромагнетика (ФМ) (спінової, пружною і електромагнітної) була теоретично доведена можливість зміни КО ЕМВ від поверхні ФМ від одиниці (повне відображення хвиль) до нуля (повне поглинання хвиль) при зміні зовнішніх параметрів (наприклад, магнітного поля або температури). У цих роботах також була показана принципова можливість управління за допомогою зовнішнього магнітного поля КО ЕМВ від поверхні ФМ в широкому інтервалі частот аж до гігагерцовий. З фізичної точки зору аномальна зміна КО ЕМВ обумовлено ефектом аномального збільшення динамічної магнітної проникності в області ФМ, магнітоакустичні або магнітостатіческого резонансів, а також при зменшенні частоти спінових хвиль за рахунок зменшення сумарної магнітної анізотропії в області ОФП [ 3 ]. В результаті, в області резонансів і поблизу ОФП поведінку динамічної магнітної сприйнятливості стає аномальним, що, в свою чергу, призводить до аномального зменшення швидкості ЕМВ і аномально великий або аномально малої здатності, що відображає ФМ.
У роботах [ 3 , 4 ] Було розглянуто випадок відображення ЕМВ від напівнескінченного ФМ. Однак на практиці і в експерименті використовуються не напівнескінченної, а зразки кінцевої товщини. Останнім часом інтенсивно досліджуються багатошарові системи з ФМ шарів, розділених проводить прошарком з товщиною менше скін-шару. Структури, утворені чергуванням шарів металу і магнетика, є новим класом шаруватих середовищ з унікальними електронними та магнітними властивостями, що залежать як від типу матеріалів, що входять в надструктури, так і від їх товщини. Тому становить інтерес досліджувати, як ці властивості впливають на магнітну проникність і відбивну здатність таких структур. Сучасні технології виготовлення шаруватих структур (такі, як молекулярно-променева епітаксії) дозволяють наносити шари атомної товщини і тим самим управляти її властивостями. Слід також зазначити, що повний аналіз властивостей таких структур неможливий і без вирішення питання про механізм взаємодії ФМ шарів через які проводять прошарку. Таким механізмом, що забезпечує сильнодіючу зв'язок між локалізованими спинами, які перебувають на кордонах сусідніх магнітних шарів, може служити непрямий обмін Руддермана-Кіттеля-Касуйі-Іосіда (РККІ) [ 6 , 7 ] Через електрони провідності проводять прошарків.
Все це призводить до цілого ряду цікавих з практичної точки зору нових фізичних явищ в розглянутих системах.
У даній роботі теоретично вивчені КО ЕМВ і інтегральна магнітна сприйнятливість шаруватої структури, що складається з взаємодіючих між собою діелектричних ФМ шарів з антипаралельними напрямком намагніченностей в них, розділених немагнітними проводять (НМП) прошарками.
2. Випадок двох ФМ шарів
Розглянемо спочатку структуру, що складається з двох ФМ шарів (N = 2) і одного НМП шару між ними, що знаходиться в зовнішньому магнітному полі. В цьому випадку можна аналітично отримати дисперсійні рівняння для ФМ шарів. Величина обмінної зв'язку між локалізованими поверхневими спинами магнітних шарів за рахунок перенесення електронів провідності провідника сильно залежить від товщини провідної прошарку [ 6 , 7 ], Тому, щоб її вплив був значним, товщину прошарку необхідно вибирати близько 10 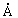 [ 8 ]. Резонансні особливості на частотних залежностях КО ЕМВ проявляються особливо чітко в разі, коли розглянута структура знаходиться на полубесконечной немагнітної провідному середовищі ( Мал. 1 ). Припустимо, що ФМ шари еквівалентні один одному і відрізняються лише напрямком намагніченості. абсолютна величина
[ 8 ]. Резонансні особливості на частотних залежностях КО ЕМВ проявляються особливо чітко в разі, коли розглянута структура знаходиться на полубесконечной немагнітної провідному середовищі ( Мал. 1 ). Припустимо, що ФМ шари еквівалентні один одному і відрізняються лише напрямком намагніченості. абсолютна величина 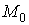 намагніченості
намагніченості  ФМ шару є постійною і спрямована в одному шарі по осі
ФМ шару є постійною і спрямована в одному шарі по осі 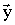 , А в іншому - в протилежному напрямку. ось
, А в іншому - в протилежному напрямку. ось 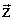 системи координат спрямуємо вздовж нормалі
системи координат спрямуємо вздовж нормалі 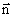 до площин розділу середовищ. Постійне магнітне поле
до площин розділу середовищ. Постійне магнітне поле 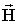 ||
|| 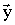 . Товщини ФМ шарів рівні l, а товщина НМП прошарків lm. Будемо розглядати нормальне падіння плоскої лінійно поляризованої ЕМВ
. Товщини ФМ шарів рівні l, а товщина НМП прошарків lm. Будемо розглядати нормальне падіння плоскої лінійно поляризованої ЕМВ 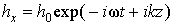 на поверхню структури.
на поверхню структури.
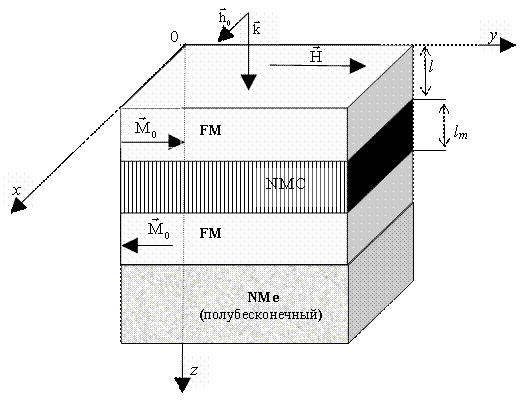
Мал. 1. Схема шаруватої структури: FM -ферромагнітний шар, NMC -немагнітний провідний шар, NMe -полубесконечная немагнітна металева середу.
Дослідження КО ЕМВ проведемо методом, заснованим на вирішенні пов'язаної системи рівнянь Максвелла і Ландау - Ліфшиця спільно з граничними умовами на вектори напруженості і індукції електромагнітного поля і на намагніченість [ 3 - 5 ]. Спільне цих рівнянь з використанням виразу для вільної енергії F шаруватої структури в розрахунку на одиницю площі і граничних умов дозволяє отримати повну пов'язану систему лінеаризованих рівнянь для визначення спектра пов'язаних коливань в ФМ шарах, швидкості поширення збуджень, вирази для інтегральної магнітної сприйнятливості і для КО ЕМВ.
Магнітну частину енергії тришарової структури (N = 2) в розрахунку на одиницю площі можна записати в такий спосіб [ 8 ]
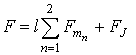 , (1)
, (1)
де 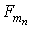 - щільність магнітної енергії n - го (в цьому розділі індекс n = 1,2) ФМ шару,
- щільність магнітної енергії n - го (в цьому розділі індекс n = 1,2) ФМ шару, 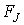 -енергія межслойного взаємодії. Як магнетика виберемо ФМ кубічної симетрії. У цьому випадку щільність магнітної енергії для n -го ФМ шару буде мати вигляд [ 3 - 5 ]
-енергія межслойного взаємодії. Як магнетика виберемо ФМ кубічної симетрії. У цьому випадку щільність магнітної енергії для n -го ФМ шару буде мати вигляд [ 3 - 5 ]
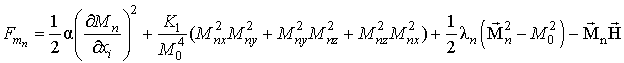 , (2)
, (2)
де 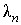 - множник Лагранжа, відповідний умові
- множник Лагранжа, відповідний умові 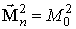 ,
, 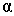 - постійна неоднорідного обміну, K 1-перша константа кубічної анізотропії,
- постійна неоднорідного обміну, K 1-перша константа кубічної анізотропії, 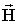 - зовнішнє магнітне поле. Енергію взаємодії між ФМ шарами врахуємо в рамках моделі біквадратичних межслойного обміну [ 8 ]
- зовнішнє магнітне поле. Енергію взаємодії між ФМ шарами врахуємо в рамках моделі біквадратичних межслойного обміну [ 8 ]
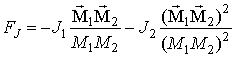 , (3)
, (3)
тут J1 і J2 - константи білінійної і біквадратичних обміну, 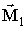 і
і 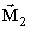 - намагніченості ФМ шарів (розглядається випадок |
- намагніченості ФМ шарів (розглядається випадок | 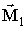 | = |
| = | 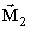 | = M 0).
| = M 0).
Рівноважний напрямок намагніченості в ФМ шарах знаходиться з умови мінімуму енергії ( 1 ) - ( 3 ) - рівності нулю перших похідних і не заперечності матриці других похідних вільної енергії. Для розглянутої колінеарний антиферомагнітної (АФМ) структури виходять такі умови її існування
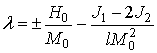 ,
, 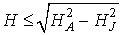 , (4)
, (4)
де 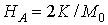 ,
, 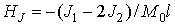 ,
, 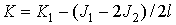 . Тут і далі верхні знаки відповідають першому ФМ шару (непарних верствам в подальших розділах), нижні - другого (парних верствам в подальших розділах). Знак рівності в нерівності (4) відповідає точці ОФП першого роду
. Тут і далі верхні знаки відповідають першому ФМ шару (непарних верствам в подальших розділах), нижні - другого (парних верствам в подальших розділах). Знак рівності в нерівності (4) відповідає точці ОФП першого роду  з колінеарну АФМ стану в неколінеарна АФМ фазу.
з колінеарну АФМ стану в неколінеарна АФМ фазу.
При відсутності зовнішнього магнітного поля і анізотропії умова стійкості для АФМ структури має вигляд: 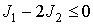 . Далі буде розглядатися саме таке співвідношення між константами білінійної і біквадратичних обміну.
. Далі буде розглядатися саме таке співвідношення між константами білінійної і біквадратичних обміну.
з ( 4 ) Видно, що міжшарове взаємодія призводить до збільшення області існування даної АФМ структури в зовнішньому магнітному полі. Таким чином, можна зробити висновок, що АФМ шарувата структура при обліку межслойного взаємодії стає більш стійкою в зовнішньому полі.
Для отримання законів дисперсії пов'язаних хвиль в ФМ шарах скористаємося системою рівнянь Максвелла і Ландау - Ліфшиця.
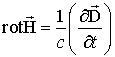 ,
, 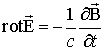 ,
,
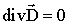 ,
, 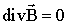 ;
;
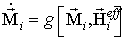 ,
,
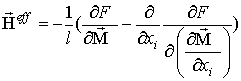 ,
,
де 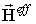 - ефективне магнітне поле,
- ефективне магнітне поле, 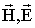 - напруженості магнітного і електричного полів відповідно,
- напруженості магнітного і електричного полів відповідно, 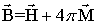 - індукція магнітного поля,
- індукція магнітного поля, 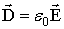 - індукція електричного поля,
- індукція електричного поля, 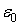 - статична діелектрична проникність,
- статична діелектрична проникність, 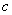 - швидкість світла у вакуумі,
- швидкість світла у вакуумі, 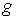 - гіромагнітне відношення. Після лінеаризації цієї системи рівнянь за допомогою методу малих коливань (
- гіромагнітне відношення. Після лінеаризації цієї системи рівнянь за допомогою методу малих коливань ( 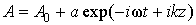 , A << A 0), отримаємо
, A << A 0), отримаємо
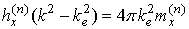 ,
, 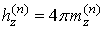
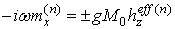 ,
, 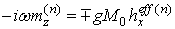 (5)
(5)
де 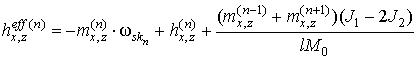 . Тут, в цьому розділі, індекс n = 1,2 відповідає 1-му і 2-му ФМ верствам,
. Тут, в цьому розділі, індекс n = 1,2 відповідає 1-му і 2-му ФМ верствам,  ,
, 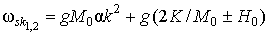 ,
, 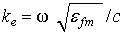 . З линеаризованной системи рівнянь ( 5 ) Можна отримати дисперсійне рівняння хвиль, що поширюються в магнітних шарах. Воно має вигляд
. З линеаризованной системи рівнянь ( 5 ) Можна отримати дисперсійне рівняння хвиль, що поширюються в магнітних шарах. Воно має вигляд
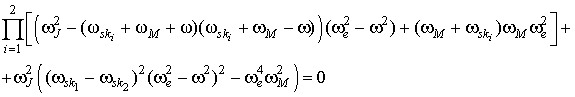 (6)
(6)
де 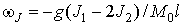 ,
, 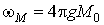 ,
, 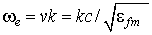 - закон дисперсії невзаимодействующих ЕМВ в ФМ шарах.
- закон дисперсії невзаимодействующих ЕМВ в ФМ шарах.
З дисперсійного рівняння ( 6 ) Слід, що одна з частот зв'язаних коливань при k = 0 звертається в нуль в точці ОФП 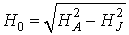 . З аналізу дисперсійного рівняння також випливає, що дві з чотирьох пов'язаних гілок коливань в даній структурі є безактіваціоннимі, а решта - активаційними. При k ® 0 закон дисперсії однієї з безактіваціонних гілок в точці ОФП (тобто при H = H 0) має лінійний характер, а інший - квадратичний
. З аналізу дисперсійного рівняння також випливає, що дві з чотирьох пов'язаних гілок коливань в даній структурі є безактіваціоннимі, а решта - активаційними. При k ® 0 закон дисперсії однієї з безактіваціонних гілок в точці ОФП (тобто при H = H 0) має лінійний характер, а інший - квадратичний
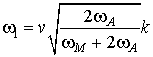 ,
, 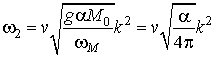 , (7)
, (7)
де 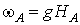 . Відзначимо, що за аналогією зі зв'язаними Магнітопружний хвилями [ 9 ], Дані гілки носять квазіелектромагнітний характер. Таким чином, з ( 7 ) Слід, що в точці ОФП швидкість однієї з гілок квазіелектромагнітних коливань істотно зменшується, а другий - прямує до нуля при k ® 0. активації інших двох гілок пов'язаних коливань в точці ОФП мають вигляд
. Відзначимо, що за аналогією зі зв'язаними Магнітопружний хвилями [ 9 ], Дані гілки носять квазіелектромагнітний характер. Таким чином, з ( 7 ) Слід, що в точці ОФП швидкість однієї з гілок квазіелектромагнітних коливань істотно зменшується, а другий - прямує до нуля при k ® 0. активації інших двох гілок пов'язаних коливань в точці ОФП мають вигляд
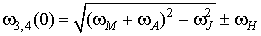 , (8)
, (8)
де 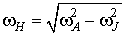 . Формула ( 8 ) Має місце і поза точки ОФП. В цьому випадку
. Формула ( 8 ) Має місце і поза точки ОФП. В цьому випадку 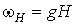 .
.
Рішенням дисперсійного рівняння ( 6 ) Щодо хвильового числа є дванадцять значень, що відповідають шести пов'язаних хвилях, які можуть поширюватися всередині кожного ФМ шару уздовж і проти осі 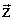 . з ( 6 ) Слід, що число пов'язаних хвиль при обліку взаємодії з сусіднім ФМ шаром збільшується вдвічі, таким чином, розглянута структура аналогічна системі двох зв'язаних осциляторів, власна частота кожного з яких збігається з частотою невзаимодействующих шарів. Отже, зі збільшенням числа шарів в структурі збільшується і число пов'язаних хвиль в кожному шарі.
. з ( 6 ) Слід, що число пов'язаних хвиль при обліку взаємодії з сусіднім ФМ шаром збільшується вдвічі, таким чином, розглянута структура аналогічна системі двох зв'язаних осциляторів, власна частота кожного з яких збігається з частотою невзаимодействующих шарів. Отже, зі збільшенням числа шарів в структурі збільшується і число пов'язаних хвиль в кожному шарі.
У НМП шарах поширюються невзаимодействующие ЕМВ уздовж і проти осі 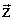 з законом дисперсії
з законом дисперсії  ,
, 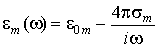 де
де 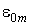 ,
, 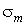 - статична проникність і електропровідність НМП прошарку.
- статична проникність і електропровідність НМП прошарку.
3. Випадок багатошарової структури
Як було показано вище, число пов'язаних хвиль усередині ФМ шарів пропорційно кількості ФМ шарів в структурі. Також з ростом N зменшується "прозорість" шаруватої структури, тому представляє інтерес подальший розрахунок проводити для випадку структури, що складається з N ФМ шарів і N - 1 НМП прошарків, що знаходяться між магнітними шарами. При цьому врахуємо тільки взаємодія між сусідніми шарами. Також припустимо, що в непарному магнітному шарі намагніченість спрямована по осі 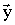 , А в парному - у протилежному напрямку. Число шарів в структурі з намагніченістю уздовж осі
, А в парному - у протилежному напрямку. Число шарів в структурі з намагніченістю уздовж осі 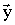 дорівнює числу шарів з намагніченістю проти осі
дорівнює числу шарів з намагніченістю проти осі 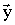 (N - парне). Магнітну частину енергії багатошарової структури в розрахунку на одиницю площі можна записати в такий спосіб [ 6 ]
(N - парне). Магнітну частину енергії багатошарової структури в розрахунку на одиницю площі можна записати в такий спосіб [ 6 ]
![Магнітну частину енергії багатошарової структури в розрахунку на одиницю площі можна записати в такий спосіб [ 6 ]](/wp-content/uploads/2020/03/uk-vidobrazenna-elektromagnitnoi-hvili-vid-periodicnoi-strukturi-so-mistit-feromagnitni-sari-64.gif)
Відзначимо, що, оскільки ФМ шар всередині структури взаємодіє одночасно з двома сусідніми ФМ шарами, а перший і останній ФМ шари взаємодіють лише з одним сусіднім ФМ шаром, то енергія межслойного взаємодії першого і останнього шарів в два рази менше, ніж для внутрішніх шарів. З огляду на це для внутрішніх шарів в умови існування АФМ структури ( 4 ) Необхідно замінити J 1 -2 J 2 на 2 (J 1 -2 J 2). Таким чином, умови існування рівноважного стану в крайніх і внутрішніх ФМ шарах відрізняються.
У загальному випадку аналітично отримати дисперсійне рівняння багатошарової структури з N> 2 неможливо, тому всі розрахунки для таких структур проводилися тільки чисельно. Рішенням дисперсійного рівняння ( 6 ) Щодо хвильового числа є 6 N значень, що відповідають 3 N пов'язаним хвилях, які можуть поширюватися всередині кожного ФМ шару уздовж і проти осі 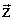 .
.
На поверхнях ФМ шарів повинні виконуватися умови безперервності тангенціальних складових векторів напруженостей і нормальних компонент векторів індукції електричного і магнітного полів, а також рівність нулю похідної намагніченості [ 3 - 5 ]. Нехай в області ![На поверхнях ФМ шарів повинні виконуватися умови безперервності тангенціальних складових векторів напруженостей і нормальних компонент векторів індукції електричного і магнітного полів, а також рівність нулю похідної намагніченості [ 3 - 5 ]](/wp-content/uploads/2020/03/uk-vidobrazenna-elektromagnitnoi-hvili-vid-periodicnoi-strukturi-so-mistit-feromagnitni-sari-65.gif) поширюються падаюча (
поширюються падаюча ( 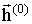 ,
, 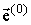 ) І відображена (
) І відображена (  ,
,  ) Хвилі, а в області
) Хвилі, а в області 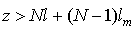 - пройшла в напівнескінченної немагнітну провідне середовище хвиля (
- пройшла в напівнескінченної немагнітну провідне середовище хвиля ( 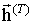 ,
, 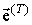 ). Позначимо хвилі, що поширюються в n-му магнітному шарі, через
). Позначимо хвилі, що поширюються в n-му магнітному шарі, через 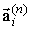 , Де i = 1 ¸ 3 N для хвиль, що поширюються уздовж нормалі до поверхні структури, i = (3 N +1) ¸ 6 N для хвиль, що поширюються в протилежному напрямку, а в n-му провіднику - через
, Де i = 1 ¸ 3 N для хвиль, що поширюються уздовж нормалі до поверхні структури, i = (3 N +1) ¸ 6 N для хвиль, що поширюються в протилежному напрямку, а в n-му провіднику - через 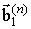 і
і 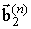 відповідно. Для зручності вихідну систему граничних умов перетворимо наступним чином. Для кожного ФМ шару граничні умови, що накладаються на електромагнітне поле і намагніченість, на верхній межі шару складемо (з позитивним і негативним знаком відповідно) з граничними умовами, що накладаються на електромагнітне поле і намагніченість, на нижній межі шару. В цьому випадку система граничних умов для n -ого (n = 1 ¸ N) магнітного шару може бути записана наступним чином.
відповідно. Для зручності вихідну систему граничних умов перетворимо наступним чином. Для кожного ФМ шару граничні умови, що накладаються на електромагнітне поле і намагніченість, на верхній межі шару складемо (з позитивним і негативним знаком відповідно) з граничними умовами, що накладаються на електромагнітне поле і намагніченість, на нижній межі шару. В цьому випадку система граничних умов для n -ого (n = 1 ¸ N) магнітного шару може бути записана наступним чином.
для 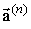 = {Hx (n), ey (n)}
= {Hx (n), ey (n)}

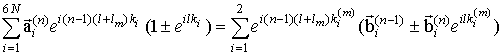 , (9)
, (9)
де на верхній межі структури 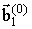 = {H (0), e (0)},
= {H (0), e (0)}, 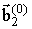 = {H (R), e (R)}, на внутрішніх кордонах
= {H (R), e (R)}, на внутрішніх кордонах  = {
= { 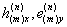 }, А на нижній межі
}, А на нижній межі 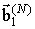 = {H (T), e (T)},
= {H (T), e (T)}, 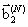 = 0.
= 0.
для 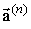 = {Mx (n), mz (n)}
= {Mx (n), mz (n)}
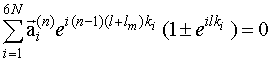 , (10)
, (10)
індекс m в виразах ( 9 ) І ( 10 ) Вказує на параметри НМП шару.
Висловлюючи з линеаризованной системи пов'язаних рівнянь ( 5 ) Компоненти намагніченості (mx (n), mz (n)) і напруженості електричного поля (ey (n)) через компоненти напруженості магнітного поля (hx (n)) і підставляючи їх в граничні умови ( 9 ) І ( 10 ), Отримаємо систему рівнянь, що містить тільки компоненти напруженості магнітного поля. З даної системи при використанні коренів дисперсійного рівняння ( 6 ) Можна визначити КО
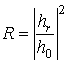 . (11)
. (11)
і 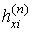 - компоненти напруженості магнітного поля в n-му ФМ шарі.
- компоненти напруженості магнітного поля в n-му ФМ шарі.
знаючи ![знаючи , Зворотним шляхом з ( 5 ) Можна розрахувати , і, отже, можна обчислити компоненти інтегральної сприйнятливості даної структури для кожного магнітного шару , Які визначаються як коефіцієнти пропорційності між компонентами інтегральної намагніченості і компонентами зовнішнього магнітного поля ( ) [ 10 ] І для всієї структури в цілому](/wp-content/uploads/2020/03/uk-vidobrazenna-elektromagnitnoi-hvili-vid-periodicnoi-strukturi-so-mistit-feromagnitni-sari-87.gif) , Зворотним шляхом з ( 5 ) Можна розрахувати
, Зворотним шляхом з ( 5 ) Можна розрахувати 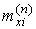 ,
,  і, отже, можна обчислити компоненти інтегральної сприйнятливості даної структури для кожного магнітного шару
і, отже, можна обчислити компоненти інтегральної сприйнятливості даної структури для кожного магнітного шару 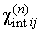 , Які визначаються як коефіцієнти пропорційності між компонентами інтегральної намагніченості і компонентами зовнішнього магнітного поля (
, Які визначаються як коефіцієнти пропорційності між компонентами інтегральної намагніченості і компонентами зовнішнього магнітного поля (  ) [ 10 ] І для всієї структури в цілому
) [ 10 ] І для всієї структури в цілому 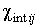
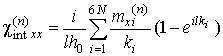 ,
, 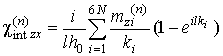 ,
, 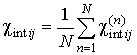 . (12)
. (12)
Розрахунок КО ЕМВ проводився чисельно. Спочатку з дисперсійного рівняння ( 6 ) Визначалися хвильові числа зв'язаних хвиль, що поширюються в ФМ шарах. Отримані значення хвильових чисел підставлялися в систему граничних умов ( 9 ) - ( 10 ). Далі дана система вирішувалася щодо амплітуди відбитої хвилі і за формулою ( 11 ) Обчислювався КО. Для розрахунку інтегральної сприйнятливості перебували компоненти напруженості магнітного поля всередині ФМ шарів, через них, використовуючи систему пов'язаних рівнянь ( 5 ) Для ФМ шару, визначалися компоненти намагніченості і за формулою ( 12 ) Остаточно обчислювалася інтегральна магнітна сприйнятливість структури.
При чисельних розрахунках для всіх структур використовувалися наступні значення постійних, типових для провідних ФМ кубічної симетрії (феритів): 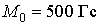 ,
, 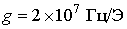 ,
, 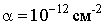 ,
, 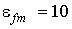 ;
; 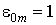 ,
, 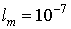 см,
см, 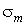 = 2.5 '1016 с-1 - для НМП шару;
= 2.5 '1016 с-1 - для НМП шару; 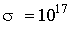 с-1 - для немагнітної полубесконечной провідного середовища. Постійні межслойного взаємодії у всіх розрахунках покладалися наступними: J 1 = - 0.5 ерг / см2, J 2 = -0.15 ерг / см2 [ 6 ].
с-1 - для немагнітної полубесконечной провідного середовища. Постійні межслойного взаємодії у всіх розрахунках покладалися наступними: J 1 = - 0.5 ерг / см2, J 2 = -0.15 ерг / см2 [ 6 ].
4. Обговорення результатів
Відзначимо, що з ( 4 ) І ( 6 ) Слід, що інтенсивність впливу межслойного обмінного взаємодії на характеристики розглянутих структур залежить від товщини шарів. Оскільки при чисельних розрахунках постійні межслойного обмінного взаємодії J 1,2 бралися порядку - (0.1 ¸ 0.5) ерг / см3, то це означає, що має сенс розглядати тільки структури з такими товщинами ФМ шарів, при яких міжшарове взаємодія порівняно з магнітною анізотропією: 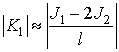 . Тому, при численних розрахунках константа анізотропії покладалася рівною До 1 = 103 ерг / см3, а товщина всіх шарів бралася рівною l = 10-4 см. У цьому випадку розглядається основний стан є стійким в полях
. Тому, при численних розрахунках константа анізотропії покладалася рівною До 1 = 103 ерг / см3, а товщина всіх шарів бралася рівною l = 10-4 см. У цьому випадку розглядається основний стан є стійким в полях 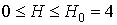 Е при відсутності межслойного взаємодії і в полях
Е при відсутності межслойного взаємодії і в полях 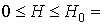
 Е »6.9 Е при наявності межслойного взаємодії.
Е »6.9 Е при наявності межслойного взаємодії.
Частотні залежності компонент інтегральної сприйнятливості тришарової структури при H = 1 Е представлені на Мал. 2 . З аналізу дисперсійного рівняння ( 6 ) Слід, що спостережуване на Мал. 2 аномальна поведінка інтегральної сприйнятливості на частотної залежності має місце в областях ФМ резонансу в магнітних шарах. В області інших частот сприйнятливість не відчуває ніяких особливостей.

Мал. 2. Залежність реальної та уявної частини компонент 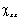 (A, b) і
(A, b) і  (C, d) інтегральної сприйнятливості від частоти. Тут і далі суцільні криві - залежно для випадку взаємодіючих (J 1,2
(C, d) інтегральної сприйнятливості від частоти. Тут і далі суцільні криві - залежно для випадку взаємодіючих (J 1,2 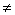 0) шарів, а пунктирні криві - залежно для випадку невзаимодействующих (J 1,2 = 0) шарів. Магнітне поле H = 1 Е Е, К 1 = 103 ерг / см3,
0) шарів, а пунктирні криві - залежно для випадку невзаимодействующих (J 1,2 = 0) шарів. Магнітне поле H = 1 Е Е, К 1 = 103 ерг / см3, 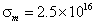 с-1, N = 2.
с-1, N = 2.
на Мал. 3 a . представлені залежності КО від частоти при різніх значення електропровідності, на Мал. 3 b - від електропровідності, на Мал. 3 c - від Товщина провідного шару в області ОФП структури. Аналіз частотної залежності КО (рис. 3а) показує, що при частотах менших 107 с-1 КО мінімальний і практично не залежить від частоти. У цій області частот на залежностях КО від електропровідності (рис. 3 b) і товщини шарів (рис. 3 c) спостерігаються чітко виражені мінімуми, що не має місця на більш високих частотах. Це обумовлено тим, що при деякому співвідношенні електропровідності і товщини провідного шару ( 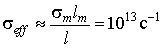 ) В області низьких частот виконується умова
) В області низьких частот виконується умова 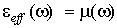 , де
, де 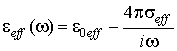 . На резонансах в області високих частот (рис. 3а) КО тим менше, чим вище електропровідність.
. На резонансах в області високих частот (рис. 3а) КО тим менше, чим вище електропровідність.
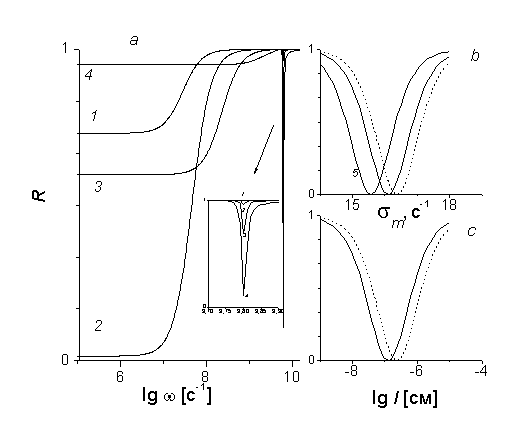
Мал. 3. Залежність КО ЕМВ в точці ОФП: (a) -від частоти для різних значень електропровідності проводять прошарків 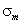 : 1 -
: 1 - 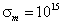 з 1; 2 -
з 1; 2 - 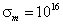 з 1; 3
з 1; 3 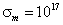 з 1; 4
з 1; 4 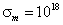 с-1 при l = 10-4 см, N = 2; (B) -від електропровідності
с-1 при l = 10-4 см, N = 2; (B) -від електропровідності 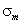 при ω = 105 с-1, l = 10-4, N = 2 (5 - для N = 8); (C) -від товщини ФМ слоевпрі ω = 105 с-1,
при ω = 105 с-1, l = 10-4, N = 2 (5 - для N = 8); (C) -від товщини ФМ слоевпрі ω = 105 с-1, 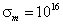 с-1, N = 2
с-1, N = 2
на Мал. 4 показана польова залежність дійсної частини компоненти 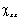 інтегральної сприйнятливості для двох значень частоти. Видно, що в області низьких частот сприйнятливість резонансно зростає по модулю в області поля ОФП. При збільшенні частоти резонанс зміщується в область малих полів, таким чином, що при ще більших частотах на польовий залежності сприйнятливості не проявляється ніяких особливостей. З рис. 4 також випливає, що облік межслойного взаємодії дійсно призводить до зміщення точки ОФП в область більш сильних полів.
інтегральної сприйнятливості для двох значень частоти. Видно, що в області низьких частот сприйнятливість резонансно зростає по модулю в області поля ОФП. При збільшенні частоти резонанс зміщується в область малих полів, таким чином, що при ще більших частотах на польовий залежності сприйнятливості не проявляється ніяких особливостей. З рис. 4 також випливає, що облік межслойного взаємодії дійсно призводить до зміщення точки ОФП в область більш сильних полів.
Мал. 4. Залежність реальної частини 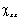 компоненти інтегральної сприйнятливості від зовнішнього поля для різних частот: 1 - ω = 108 с-1, 2 - ω = 3 '109 с-1 при К 1 = 103 ерг / см3, l = 10-4 см,
компоненти інтегральної сприйнятливості від зовнішнього поля для різних частот: 1 - ω = 108 с-1, 2 - ω = 3 '109 с-1 при К 1 = 103 ерг / см3, l = 10-4 см, 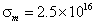 с-1, N = 2.
с-1, N = 2.
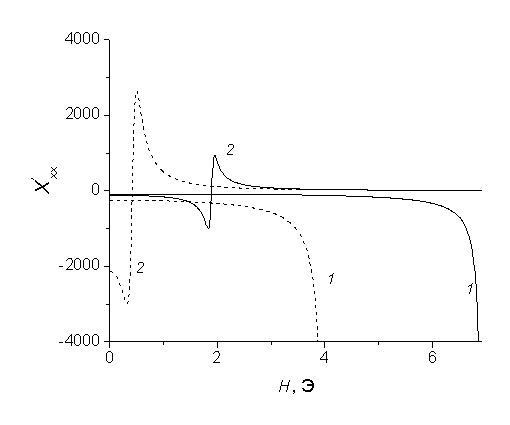
на Мал. 5а, 5 b наведені результати чисельного розрахунку інтегральної сприйнятливості і КО для шаруватої структури (N = 2) при К 1 = 103 ерг / см3, l = 1 '10-4 см в області ОФП, а на рис 5с, 5 d - при малому зовнішньому магнітному полі 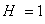 Е. Нагадаємо, що при таких значеннях константи анізотропії і товщини шарів поле ОФП в парних ФМ шарах дорівнює 4 Е і 6.9 Е відповідно при відсутності і наявності межслойного взаємодії. З рис. 5 видно, що КО різко зменшується в області аномального поведінки інтегральної сприйнятливості, тобто в області ФМ резонансів в ФМ шарах. Також видно, що наявність межслойного взаємодії призводить до зміщення піків КО. При наближенні до точки ОФП (рис. 5) відбувається зміщення резонансної частоти парних ФМ шарів в сторону низьких частот і розширення піка КО. Це призводить до того, що поблизу ОФП при низьких частотах КО дорівнює нулю, тобто система перетворюється з повністю відбиває в повністю поглинає.
Е. Нагадаємо, що при таких значеннях константи анізотропії і товщини шарів поле ОФП в парних ФМ шарах дорівнює 4 Е і 6.9 Е відповідно при відсутності і наявності межслойного взаємодії. З рис. 5 видно, що КО різко зменшується в області аномального поведінки інтегральної сприйнятливості, тобто в області ФМ резонансів в ФМ шарах. Також видно, що наявність межслойного взаємодії призводить до зміщення піків КО. При наближенні до точки ОФП (рис. 5) відбувається зміщення резонансної частоти парних ФМ шарів в сторону низьких частот і розширення піка КО. Це призводить до того, що поблизу ОФП при низьких частотах КО дорівнює нулю, тобто система перетворюється з повністю відбиває в повністю поглинає.
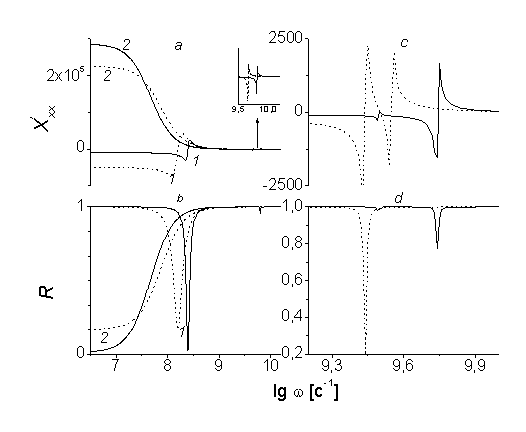
Мал. 5. Залежність реальної частини 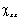 компоненти інтегральної сприйнятливості (a, c) і КО ЕМВ (b, d) від частоти для різних значень зовнішнього магнітного поля Н. a, b: 1 - поблизу ОФП3.99 Е, пунктирна крива (невзаимодействующие шари), 6.9 Е, суцільна крива (взаємодіючі шари); 2 - в точці ОФП4 Е, пунктирна крива,
компоненти інтегральної сприйнятливості (a, c) і КО ЕМВ (b, d) від частоти для різних значень зовнішнього магнітного поля Н. a, b: 1 - поблизу ОФП3.99 Е, пунктирна крива (невзаимодействующие шари), 6.9 Е, суцільна крива (взаємодіючі шари); 2 - в точці ОФП4 Е, пунктирна крива, 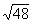 Е, суцільна крива. c, d - 1 Е. До 1 = 103 ерг / см3, l = 10-4 см,
Е, суцільна крива. c, d - 1 Е. До 1 = 103 ерг / см3, l = 10-4 см, 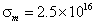 с-1, N = 2.
с-1, N = 2.
Для того, щоб резонансні частотні області зменшення КО були ширші, необхідно збільшувати товщину шаруватої структури в цілому. Це можна сделать декількома способами.
Перший спосіб - збільшення числа шарів. При цьому для значення постійної анізотропії К 1 = 103 ерг / см3 число шарів необхідно збільшити до 103-105. В даному випадку через взаємодію ФМ верств різко збільшується ступінь дисперсійного рівняння, що призводить до значного збільшення часу розрахунків.
Другий спосіб - збільшення товщини магнітного шару. При цьому зменшується внесок в ефективну анізотропію структури від межслойного взаємодії. Для того, щоб він залишався порівнянним з внеском від анізотропії, необхідно зменшувати і постійну магнітної анізотропії.
на Мал. 6 a, 6 b наведено результат чисельного розрахунку інтегральної сприйнятливості і КО для багатошарової структури (N = 8, К 1 = 103 ерг / см3, l = 10-4 см) в області ОФП, а на Мал. 6с, 6 d - при малому зовнішньому полі 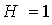 Е. Відзначимо, що при такому значенні константи анізотропії і товщини шарів поле ОФП при наявності межслойного взаємодії в нижньому ФМ шарі одно 6.9 Е, а для внутрішніх непарних шарів поле ОФП має більше значення, оскільки, як говорилося вище, енергія межслойного взаємодії першого і останнього шарів в два рази менше внутрішніх. З рис. 6 видно, що в даному випадку число резонансних піків при наявності межслойного взаємодії збільшується (пор. З Мал. 5 ). Це обумовлено тим, що при рівних товщинах поле ОФП в взаємодіючих шарах різному, а отже резонанси від різних ФМ шарів з однаковим напрямком намагніченості відрізняються один від одного по частоті.
Е. Відзначимо, що при такому значенні константи анізотропії і товщини шарів поле ОФП при наявності межслойного взаємодії в нижньому ФМ шарі одно 6.9 Е, а для внутрішніх непарних шарів поле ОФП має більше значення, оскільки, як говорилося вище, енергія межслойного взаємодії першого і останнього шарів в два рази менше внутрішніх. З рис. 6 видно, що в даному випадку число резонансних піків при наявності межслойного взаємодії збільшується (пор. З Мал. 5 ). Це обумовлено тим, що при рівних товщинах поле ОФП в взаємодіючих шарах різному, а отже резонанси від різних ФМ шарів з однаковим напрямком намагніченості відрізняються один від одного по частоті.
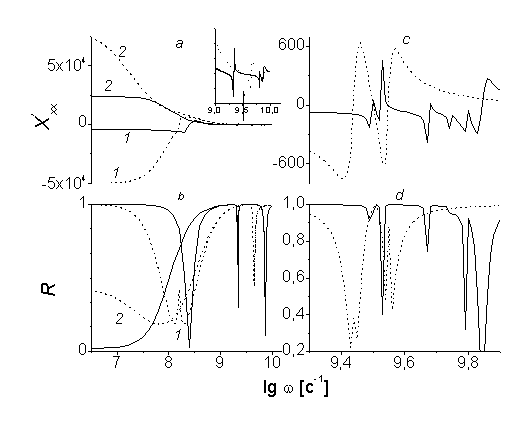
Мал. 6. теж, що на рис 5. при N = 8.
5. Висновок
Таким чином, в даній роботі теоретично досліджено вплив межслойного обмінного взаємодії на рівноважний стан, інтегральну сприйнятливість і відбивну здатність структур, що складаються з взаємодіючих між собою ФМ шарів з АФМ напрямком намагніченості щодо один одного, розділених НМП прошарками. Чисельно розраховані частотні та польові залежності інтегральної сприйнятливості і КО ЕМВ при різній кількості шарів в структурі.
Показано, що область існування АФМ шаруватої структури в зовнішньому магнітному полі при наявності межслойного взаємодії збільшується. Інтегральна сприйнятливість і КО ЕМВ мають резонансні особливості в області частот, що відповідають частотам ФМ резонансу в ФМ шарах. При цьому при наближенні до точки ОФП відбувається зміщення піку на частоті, що відповідає ФМ резонансу в шарах з протилежним по відношенню до зовнішнього поля напрямком намагніченості (парні шари), в область низьких частот і його розширення. Це призводить до того, що поблизу ОФП при низьких частотах КО дорівнює нулю, тобто система перетворюється з повністю відбиває в повністю поглинає.
Збільшення числа шарів призводить до збільшення числа резонансних піків КО і розширенню деяких з них, за рахунок накладення піків один на одного. Це обумовлено тим, що резонанси від ФМ шарів відрізняються по частоті через відмінності величини межслойного взаємодії для зовнішніх і внутрішніх шарів. В області резонансів КО близький до нуля, тобто при резонансних частотах багатошарова структура з повністю відбиває для ЕМВ розглянутого діапазону (108-1011 з-1) стає повністю поглинає. Також показано, що облік межслойного взаємодії призводить до зміщення резонансних особливостей. Все це може представляти інтерес з практичної точки зору при конструюванні пристроїв, в яких необхідно зміщувати резонансні частоти або включати нові.
Робота виконана за фінансової підтримки гранту РФФД-Урал 07_02_96030.
список літератури
[1] Казанцева Н.Є., Ривкіна Н.Г., Чмутіної І.А. // РЕ. 2003. Т. 48, №2, С. 196.
[2] Антонов А.С., Паніна Л.В., Саричев А.К. // ЖТФ. 1989. Т. 59, №6, С. 88 ,.
[3] Бучельніков В.Д., Бичков І.В., Шавров В.Г. // ФТТ. 1992. Т. 34, №11, С. 3408.
[4] Бабушкін А.В., Бучельніков В.Д., Бичков І.В. // ФТТ. 2002. Т. 44, №12, С. 2183.
[5] Бучельніков В.Д., Бабушкін А.В., Бичков І.В. // ФТТ. 2003. Т. 45, №4, С. 663.
[6] Хусаїнов М.Г. // ЖЕТФ. 1996. Т. 109, С. 524.
[7] Хусаїнов М.Г. // ЖЕТФ. 1996. Т. 110, С. 966.
[8] Дроворубів А.Б., Жотікова О.В. та ін. // ЖЕТФ. 1999. Т. 119, №5, С. 1817.
[9] Туров Е.А., Шавров В.Г. // УФН. 1983. Т. 140, №3, С. 429.
[10] Сукстанскій А.Л., Ямпільська Г.І. // ФТТ. 2000. Т. 42, №5, С. 866.




