ОСНОВИ ЕЛЕКТРОНІКИ
Повний і реактивний опір
Завдяки тому що імпеданс конденсатора, рівний Zc = -j / ωС, залежить від частоти, за допомогою конденсаторів і резисторів можна будувати частотно-залежні подільники напруги, які будуть пропускати тільки сигнали потрібної частоти, а всі інші пригнічувати. У цьому розділі ви познайомитеся з прикладами найпростіших RС-фільтрів, до яких ми будемо неодноразово звертатися в подальшому. В гл. 5 описані більш складні фільтри.
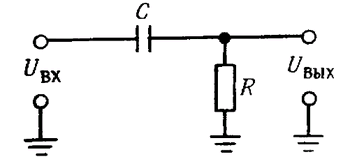
Мал. 1.52. Фільтр високих частот.
Фільтри високих частот. На рис. 1.52 показаний дільник напруги, що складається з конденсатора і резистора. Відповідно до закону Ома для комплексних величин,
I = Uвх / Zполн = Uвх / R - (j / ωC) = Uвх [R + j / ωC)] / R2 + 1 / ω2C2.
(Остаточний результат зарплат після множення чисельника і знаменника на комплексне число, поєднане знаменника.) Отже, напруга на резисторі R одно
U вих = IZR = IR = Uвх [R + (j / ωС) R] / R2 + 1 / ω2C2.
Найчастіше нас цікавить не фаза, а амплітуда U вих:
U вих = (UвихUвих *) 1/2 = UвхR / [R2 + (1 / ω2C2)] 1/2.
Порівняйте отриманий результат з виразом для резистивного дільника:
U вих = UвхR1 / (R1 + R2).
Векторне подання імпедансу RС - ланцюги (рис. 1.53) показано на рис. 1.54.
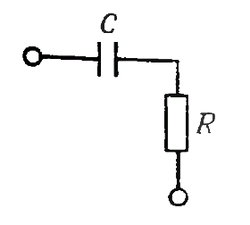
Мал. 1.53.
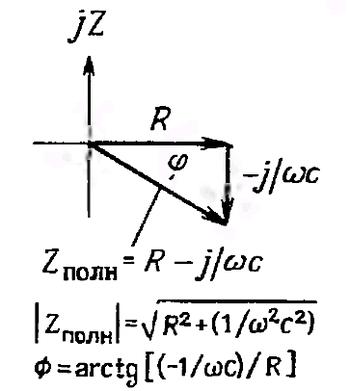
Мал. 1.54.
Отже, якщо не брати до уваги зрушення фаз, а розглядати тільки модулі комплексних амплітуд, то «відгук» схеми буде визначатися таким чином:
U вих = UвхR / [R2 + (1 / ω2C2)] 1/2 = Uвх2πƒRC / [1 + (2πƒRC)] 1/2.
Графік цієї залежності представлений на рис. 1.55. Такий же результат ми б отримали, якби визначили ставлення модулів импедансов як в вправі 1.17 і в прикладі перед цією вправою; чисельник є модуль імпедансу нижнього плеча дільника R, а знаменник - модуль імпедансу послідовного з'єднання R і С.
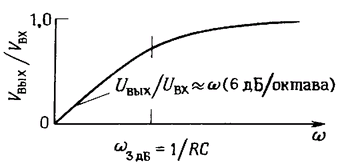
Мал. 1.55. Частотна характеристика фільтра високих частот.
Як ви бачите, на високих частотах вихідна напруга приблизно дорівнює вхідному (ω> 1 / RC), а на низьких частотах вихідна напруга зменшується до нуля. Ми прийшли до важливого результату, запам'ятайте його. Подібна схема, зі зрозумілих причин, називається фільтром високих частот. На практиці її використовують дуже широко. Наприклад, в осцилографі передбачена можливість зв'язку по змінному струмі між досліджуваної схемою і входом осцилографа. Цей зв'язок забезпечується за допомогою фільтра високих частот, що має перегин характеристики в області 10 Гц (зв'язок по змінному струмі використовують для того, щоб розглянути невеликий сигнал на тлі великого напруги постійного струму). Інженери часто користуються поняттям «точки зламу» -3 дБ для фільтра (або будь-який інший схеми, яка поводиться як фільтр)! У разі простого RC - фільтра високих частот точка зламу -3 дБ визначається виразом:
ƒ3дб = 1 / 2πRC.
Зверніть увагу, що конденсатор не пропускає струм (ƒ = 0). Найпоширеніший приклад використання конденсатора-це використання його в якості блокуючого конденсатора постійного струму. Якщо виникає необхідність забезпечити зв'язок між підсилювачами, то майже завжди вдаються до допомоги конденсатора. Наприклад, у будь-якого підсилювача звукової частоти високого класу всі входи мають ємнісний зв'язок, так як заздалегідь не відомо, який рівень постійного струму матимуть вхідні сигнали. Для забезпечення зв'язку необхідно підібрати R і С таким чином, щоб всі потрібні частоти (в даному випадку 20 Гц - 20 кГц) надходили на вхід без втрат (без поділу на вході).

Мал. 1.56. а - Зміна реактивного опору индуктивностей і конденсаторів в залежності від частоти. Все декади однакові і відрізняються лише масштабом. б - збільшення відображення однієї декади з графіка А. графік побудований для стандартних компонентів, що мають точність 20%.
Як приклад розглянемо фільтр, показаний на рис. 1.57. Це фільтр високих частот з точкою перегину 3 дБ на частоті 15,9 кГц. Імпеданс навантаження, що підключається до фільтру, повинен бути значно більше 1 кОм. інакше навантаження буде спотворювати вихідна напруга фільтра. Джерело сигналу повинен забезпечувати можливість підключення навантаження 1 кОм без значної аттенюапіі (втрати амплітуди сигналу), інакше фільтр буде спотворювати вихід джерела сигналу.

Мал. 1.57. Мал. 1.58. Фільтр низьких частот.
Фільтри низьких частот. Якщо поміняти місцями R і С (рис. 1.58), то фільтр буде вести себе протилежним чином відносно частоти. Можна показати, що U вих = [1/1 + ω2R2С2) 1/2] Uвх. Графік цієї залежності представлений на рис. 1.59. Такий фільтр називають фільтром низьких частот. Точка -3 дБ на характеристиці фільтра знаходиться на частоті ƒ = 1 / 2πRC. Фільтри низьких частот знаходять дуже широке застосування. Наприклад, їх використовують для усунення впливу довколишніх радіо - і телевізійних станцій (550 кГц - 800 МГц), на роботу підсилювачів звукових частот і інших чутливих електронних приладів.
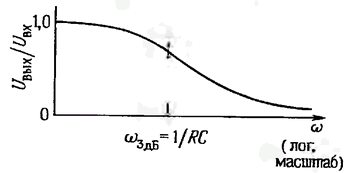
Мал. 1.59 Частотна характеристика фільтра низьких частот.
Вправа 1.21. Доведіть справедливість виразу для вихідної напруги фільтра низьких частот.
Вихід фільтра низьких частот можна розглядати в якості самостійного джерела сигналів. При використанні ідеального джерела напруги змінного струму (з нульовим опором) фільтр з боку виходу низьких частот має опір R (при розрахунках повних опорів ідеальне джерело сигналів можна замінити коротким замиканням, тобто його нульовим опором для малого сигналу). У вихідному імпедансі фільтра переважає ємнісна составляюшей. і на високих частотах він стає рівним нулю. Для вхідного сигналу фільтр являє собою навантаження, що складається на низьких частотах з опору R і опору навантаження, а на високих частотах - навантаження, яке дорівнює просто опору R.
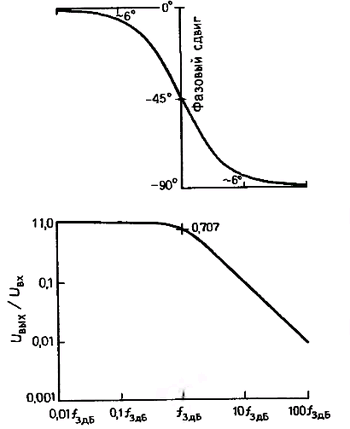
Мал. 1.60. Фазочастотная і амплітудно-частотна характеристики фільтра низьких частот, зображені в логарифмічному масштабі. У точці 3 дБ фазовий зсув становить 45 ° і в межах декади зміни частоти лежить в межах 6 ° від асимптотичного значення.
На рис. 1.60 зображена також частотна характеристика фільтра низьких частот, але в більш звичному вигляді для вертикальної і горизонтальної осей використаний логарифмічний масштаб. Можна вважати, що по вертикальній осі відкладаються децибели, а по горизонтальній - октави (або декади). На такому графіку рівні відстані відповідають рівним відносинам величин. У вигляді графіка зображений також фазовий зсув, при цьому для вертикальної осі (градуси) використаний лінійний масштаб, а для осі частот-логарифмічний. Такий графік зручний для аналізу частотної характеристики навіть у випадку значної аттенюаціі (праворуч): цілий ряд таких графіків представлений в гл. 5 , Присвяченій вивченню активних фільтрів. Відзначимо, що при значній аттенюаціі зображена на графіку крива вироджується в пряму лінію з нахилом -20 дБ / декада (інженери воліють вираз «-6 дБ / октава»). Відзначимо також, що фазовий зсув плавно змінюється від 0 ° (на частотах нижче точки перегину) до 90 ° (на частотах істотно вище точки перегину), а в точці -3 дБ складає 45 °. Практичне правило для односекційних RС - фільтрів говорить про те. що фазовий зсув становить ≈6 ° від асимптот в точках 0.1ƒ3дБ і 10ƒ3дБ.
Вправа 1.22. Доведіть останнє твердження.
Виникає цікаве питання: чи можна зробити фільтр з будь-якої іншої заданої амплітудної характеристикою і будь-якої іншої заданої фазової характеристикою. Нехай вас це не дивує, але відповісти можна тільки негативно - не можна. Фазова і амплітудна характеристики для всіх можливих фільтрів підпадають під дію законів причинного зв'язку (тобто характеристика є наслідком певних властивостей, але не їх причиною).
Частотні характеристики диференціюють і інтегрують RС - ланцюгів. Схема диференціює RС - ланцюги, яку ми розглянули в розд. 1.14 , Має такий же вигляд, як і схема фільтра високих частот, наведені в цьому розділі. Чим же вважати таку схему, залежить від того, що вас більше цікавить: перетворення сигналів в часі або частотна характеристика. Отримане раніше тимчасове умова правильної роботи схеми (U вих «Uвх) можна сформулювати інакше, стосовно частотній характеристиці: для того щоб вихідний сигнал був невеликим порівняно з вхідним, частота повинна бути значно нижче, ніж в точці -3 дБ. У цьому легко переконатися. Припустимо, що вхідний сигнал дорівнює Uвх = sinωt. Скористаємося рівнянням, яке ми отримали раніше для виходу дифференциатора:
Uвх = RC d / dt sinωt = ωRCcosωt.
Звідси U вих «Uвх, якщо ωRC« 1, тобто RC «1 / ω. Якщо вхідний сигнал містить деякий діапазон частот, то умова має виконуватися для найвищих частот вхідного діапазону.
Схема інтегруючого RC - ланцюга ( розд. 1.15 ) Має такий же вигляд, як і схема фільтра низьких частот: аналогічно в хорошому інтеграторі найнижчі частоти вхідного сигналу повинні істотно перевищувати частоту в точці -ЗдБ.
Індуктивності і конденсатори. Індуктивності, також як і конденсатори, в поєднанні з резисторами утворюють схеми фільтрів низьких (або високих) частот. Однак на практиці RL - фільтри низьких і високих частот зустрічаються рідко. Це пов'язано з тим, що індуктивності більш громіздкі і дороги, а працюють гірше, ніж конденсатори (їх характеристики більш істотно відрізняються від ідеальних). Якщо є можливість вибору, то перевагу краще віддати конденсатору. Винятком з цієї загальної рекомендації є ферритові намистини (маленькі тороїдальні осердя) і дроселі в високочастотних схемах. Кілька намистин нанизують на дріт, завдяки цьому з'єднання, виконане за допомогою дроту, стає в деякій мірі індуктивним; імпеданс на високих частотах збільшується і запобігає «коливання» в схемі, при цьому на відміну від RС - фільтра активний опір схеми не збільшується. Радіочастотний дросель - це котушка, що складається з декількох витків дроту і ферритового сердечника і використовувана з тією ж метою в радіочастотних схемах.
Діоди і діодні схеми




